Electric potential at any point is V=−5x+3y+√15z, then the magnitude of the electric field is
3√2
4√2
5√2
7
The correct Answer is:D
To find the magnitude of the electric field given the electric potential V=−5x+3y+√15z, we will follow these steps:
Step 1: Understand the relationship between electric potential and electric field
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
where ∇V is the gradient of the potential.
Step 2: Calculate the components of the electric field
The components of the electric field can be calculated using the following formulas:
- Ex=−∂V∂x
- Ey=−∂V∂y
- Ez=−∂V∂z
Step 2.1: Calculate Ex
Ex=−∂V∂x=−∂∂x(−5x+3y+√15z)=−(−5)=5
Step 2.2: Calculate Ey
Ey=−∂V∂y=−∂∂y(−5x+3y+√15z)=−3
Step 2.3: Calculate Ez
Ez=−∂V∂z=−∂∂z(−5x+3y+√15z)=−√15
Step 3: Calculate the magnitude of the electric field
The magnitude of the electric field E is given by:
E=√E2x+E2y+E2z
Substituting the values we found:
E=√(5)2+(−3)2+(−√15)2
E=√25+9+15
E=√49=7
Conclusion
The magnitude of the electric field is E=7.
---
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
where ∇V is the gradient of the potential.
The components of the electric field can be calculated using the following formulas:
- Ex=−∂V∂x
- Ey=−∂V∂y
- Ez=−∂V∂z
Ex=−∂V∂x=−∂∂x(−5x+3y+√15z)=−(−5)=5
Ey=−∂V∂y=−∂∂y(−5x+3y+√15z)=−3
Ez=−∂V∂z=−∂∂z(−5x+3y+√15z)=−√15
The magnitude of the electric field E is given by:
E=√E2x+E2y+E2z
E=√(5)2+(−3)2+(−√15)2
E=√25+9+15
E=√49=7
The magnitude of the electric field is E=7.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
If the potential function is define as V=(−3x+4y+12z)V, then magnitude of electric field E(x,y,z) is
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View SolutionThe potential at any point is given by V=x(y2−4x2). Calculate the cartesian components of the electric field at the point.
View SolutionThe variation of potential with distance x from a fixed point is shown in figure. Find the magnitude of the electric field (in V/m) at x=13m.

View SolutionThe electric potential at any point x,yandz in metres is given by V=3x2. The electric field at a point (2,0,1) is
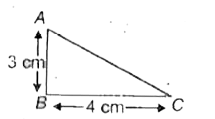
View SolutionABC is a right anlged triangle situated in a uiform electric field →E which is in the plane of the traingle . The points A and B are at the same potential of 15 V while the point C is at a potential of 20 V. AB = 3cm and BC = 4 cm . The magnitude of electric field is (in S.I . Units )
View SolutionIf on the x - axis electric potential decreases uniform from 60 V to 20 V between x = -2 m to x = +2 m then the magnitude of electric field at the origin
View SolutionThe adjoining figure shows the lines of constant potential in a region in which an electric field is present. The value of potentials are shown. At which of the points A, B and C is the magnitude of the electric field the greatest?
View SolutionThe electric potential at a space point P (X, Y, Z) is given as V=x2+y2+z2. The modulus of the electric field at that point is proportional to
View Solution
