The distance between the circular plates of a parallel plate condenser 40 mm in diameter, in order to have same capacity as a sphere of radius 1 m is
0.01 mm
0.1 mm
1.0 mm
10 mm
The correct Answer is:B
To find the distance between the circular plates of a parallel plate capacitor that has the same capacitance as a sphere of radius 1 m, we can follow these steps:
Step 1: Understand the given data
- Diameter of the parallel plate capacitor (d) = 40 mm
- Radius of the sphere (R) = 1 m
Step 2: Convert the diameter to radius
The radius (r) of the parallel plate capacitor is half of the diameter:
r=d2=40 mm2=20 mm=20×10−3 m
Step 3: Write the formula for capacitance of a parallel plate capacitor
The capacitance (C1) of a parallel plate capacitor is given by:
C1=ϵ0Ad
where A is the area of the plates and d is the distance between the plates.
The area A of the circular plates is:
A=πr2
Substituting this into the capacitance formula gives:
C1=ϵ0πr2d
Step 4: Write the formula for capacitance of a sphere
The capacitance (C2) of an isolated sphere is given by:
C2=4πϵ0R
Step 5: Set the capacitances equal to each other
Since we want the capacitance of the parallel plate capacitor to be equal to that of the sphere:
C1=C2
This leads to:
ϵ0πr2d=4πϵ0R
Step 6: Simplify the equation
We can cancel ϵ0 and π from both sides:
r2d=4R
Step 7: Solve for d
Rearranging the equation gives:
d=r24R
Step 8: Substitute the values
Substituting r=20×10−3 m and R=1 m:
d=(20×10−3)24×1
Calculating (20×10−3)2:
(20×10−3)2=400×10−6 m2
Now substituting back:
d=400×10−64=100×10−6 m
Step 9: Convert to mm
To convert meters to millimeters:
d=100×10−6 m=0.1 mm
Final Answer
The distance d between the circular plates of the parallel plate capacitor is:
0.1 mm
- Diameter of the parallel plate capacitor (d) = 40 mm
- Radius of the sphere (R) = 1 m
The radius (r) of the parallel plate capacitor is half of the diameter:
r=d2=40 mm2=20 mm=20×10−3 m
The capacitance (C1) of a parallel plate capacitor is given by:
C1=ϵ0Ad
where A is the area of the plates and d is the distance between the plates.
A=πr2
Substituting this into the capacitance formula gives:
C1=ϵ0πr2d
The capacitance (C2) of an isolated sphere is given by:
C2=4πϵ0R
Since we want the capacitance of the parallel plate capacitor to be equal to that of the sphere:
C1=C2
This leads to:
ϵ0πr2d=4πϵ0R
We can cancel ϵ0 and π from both sides:
r2d=4R
Rearranging the equation gives:
d=r24R
Substituting r=20×10−3 m and R=1 m:
d=(20×10−3)24×1
Calculating (20×10−3)2:
(20×10−3)2=400×10−6 m2
Now substituting back:
d=400×10−64=100×10−6 m
To convert meters to millimeters:
d=100×10−6 m=0.1 mm
The distance d between the circular plates of the parallel plate capacitor is:
0.1 mm
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
When a dielectric slab of thickness 6 cm is introduced between the plates of parallel plate condenser, it is found that the distance between the plates has to be increased by 4 cm to restore to capacity original value. The dielectric constant of the slab is
View SolutionStatement I: When air between the plates of a parallel plate condenser is replaced by an insulating dielectric medium, its capacity decreases.
Statement II: Electric field intensity between the plates with dielectric in between is reduced.
View SolutionA dielectric of constant K is slipped between the plates as parallel plate condenser in half of the space as shown in the figure. If the capacity of air condenser is C, then new capacitance between A and B with be-
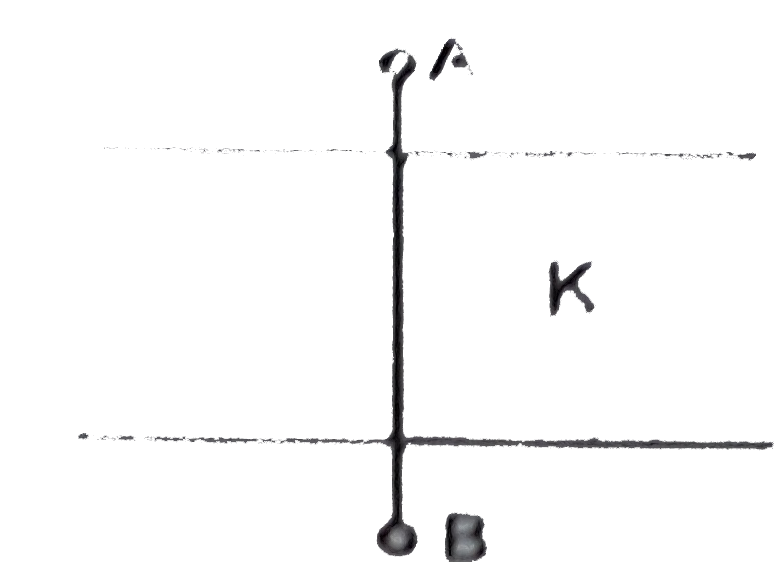
View SolutionA small conducting sphere is hanged by an insulating thread between the plates of a parallel plate capacitor as shown in figure. The net force on the sphere is
View SolutionThe distance between the plates of a parallel plate capacitor is 0.04m A field of 5000V/m is established between the plates and an unchanged metal plate of thickness 0.01m is inserted intothe condenser parallel to its plate. Find the p.d. between the plates (a) before the introducing of the metal plate and (b) after its introduction. what would be the p.d. if plate of dielectric constant K=2 is introduced in place of metal plate?
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionThe electrostatic force between the metal plate of an isolated parallel plate capacitor C having charge Q and area A, is
View Solution