A cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
To find the internal resistance of the cell, we can follow these steps:
Step 1: Define the given values
Let:
- L1=110cm (length of the potentiometer wire with the cell short-circuited)
- L2=100cm (length of the potentiometer wire without the cell short-circuited)
- R=10Ω (external resistance)
Step 2: Use the relationship between EMF and potential difference
The EMF of the cell (E) can be related to the potential difference (V) across the external resistance using the lengths of the potentiometer wire:
EV=L1L2
Step 3: Express E and V in terms of current (I) and resistances
When the cell is short-circuited:
E = I(R + r) \quad \text{(where r is the internal resistance)}
When the cell is not short-circuited:
V=IR
Step 4: Substitute the expressions into the ratio
Substituting these expressions into the ratio gives:
I(R+r)IR=L1L2
Cancelling I from both sides (assuming I≠0):
R+rR=L1L2
Step 5: Substitute the known values
Substituting L1=110 and L2=100:
R+rR=110100=1110
Step 6: Rearranging the equation
This can be rearranged to:
R+r=1110R
Subtracting R from both sides:
r=1110R−R
r=11R−10R10=R10
Step 7: Substitute R=10Ω
Now substituting R=10Ω:
r=1010=1Ω
Final Answer
The internal resistance of the cell is r=1Ω.
---
Let:
- L1=110cm (length of the potentiometer wire with the cell short-circuited)
- L2=100cm (length of the potentiometer wire without the cell short-circuited)
- R=10Ω (external resistance)
The EMF of the cell (E) can be related to the potential difference (V) across the external resistance using the lengths of the potentiometer wire:
EV=L1L2
When the cell is short-circuited:
E = I(R + r) \quad \text{(where r is the internal resistance)}
When the cell is not short-circuited:
V=IR
Substituting these expressions into the ratio gives:
I(R+r)IR=L1L2
Cancelling I from both sides (assuming I≠0):
R+rR=L1L2
Substituting L1=110 and L2=100:
R+rR=110100=1110
This can be rearranged to:
R+r=1110R
Subtracting R from both sides:
r=1110R−R
r=11R−10R10=R10
Now substituting R=10Ω:
r=1010=1Ω
The internal resistance of the cell is r=1Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A Daniel cell is balanced on 125cm length of a potentiometer wire. Now the cells is short-circuited by a resistance 2ohm and the balance is obtained at 100cm. The internal resistance of the Dainel cell is
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View SolutionA 20 m long potentiometer wire has a resistance of 20 Ohm. It is connected in series with a battery of emf 3V and resistance of 10Ω. The internal resistance of cell is negligible. If the lenth can be read accurately up to 1 mm, the potentiometer can read voltage:
View Solution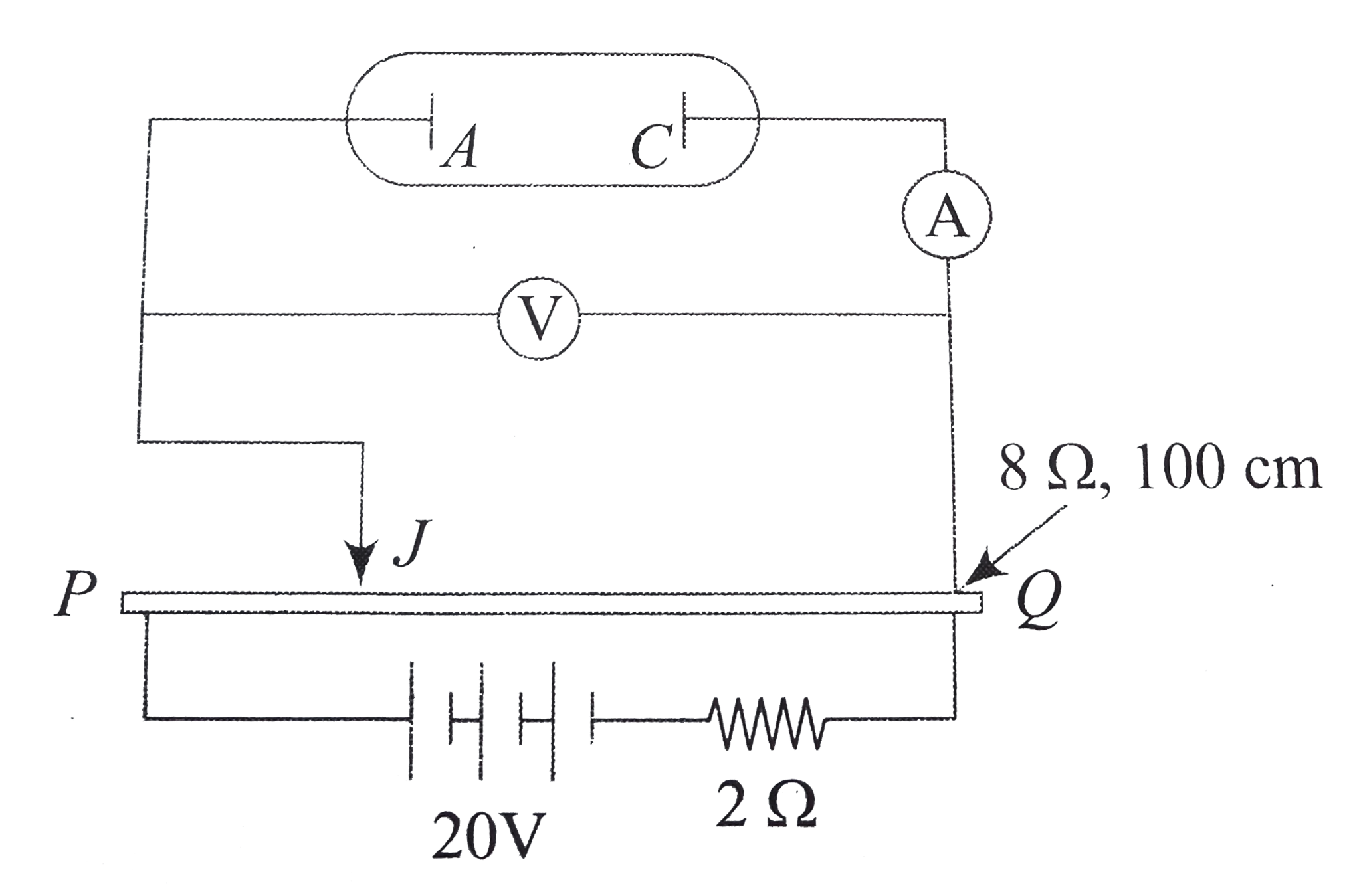
An experimental setup of verification of photoelectric effect is shown if Fig. The voltage across the electrodes is measured with the help of an ideal voltmeter, and which can be varied by moving jockey J on the potentiometer with wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2Ω. The resistance of 100 cm long potentiometer wire is 8Ω.
The photocurrent is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photocurrent in the circuit is very small, so we can treat the potentiometer circuit as an independent circuit. The wavelength of various colors is as follows:
Q. It is found that ammeter current remains unchanged (2μA) even when the jockey is moved from the end P to the middle point of the potentiometer wire. Assuming that all the incident photons eject electrons and the power of the light incident is 4×10−6 W. Then, the color of the incident light is
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionA standerd cell emf 1.08Vis balance by the potential difference across 91cm of a meter long wire applied by a cell of emf 2V through a series resistor of resistance 2Ω. The internal resistance of the cell is zero. Find the resistance per unit length of the potentiometer wire.
View SolutionA 10m long potentiometer wire has a resistance of 20 ohm. It is connected in series with a battery of emf 3V and a resistance of 10Ω. The internal resistance of cell is negligible. If he length can be read accurately up 10 1mm, the potentiometer can read voltage.
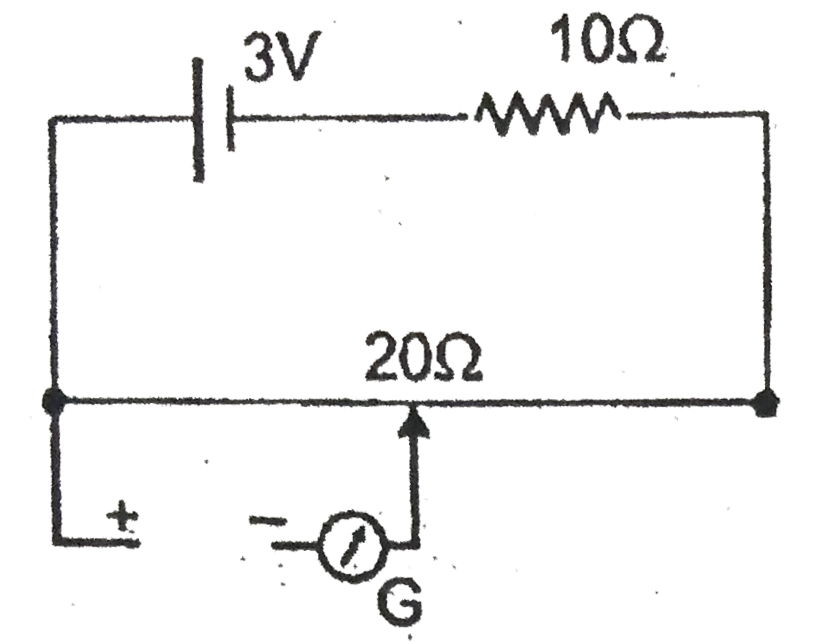
View Solution
