Two electric bulbs one, if 200 V-40 W and other 200 V-100 W are connected in series to a 200 V line, then the potential drop across
the two bulbs is the same
Both the bulbs is 200 V
40 W bulb is greater than the potential drop across 100 W bulb
100 W bulb is greater than the potential drop across 40 W bulb
The correct Answer is:C
To solve the problem of finding the potential drop across two electric bulbs connected in series, we will follow these steps:
Step 1: Determine the Resistance of Each Bulb
We know the power (P) and voltage (V) for each bulb. The resistance (R) can be calculated using the formula:
R=V2P
For the 40 W bulb:
R1=(200V)240W=4000040=1000Ω
For the 100 W bulb:
R2=(200V)2100W=40000100=400Ω
Step 2: Calculate the Total Resistance in the Circuit
Since the bulbs are connected in series, the total resistance (R_total) is the sum of the individual resistances:
Rtotal=R1+R2=1000Ω+400Ω=1400Ω
Step 3: Calculate the Current Flowing Through the Circuit
Using Ohm's Law, the current (I) in the circuit can be calculated using the total voltage (V_total) and the total resistance (R_total):
I=VtotalRtotal=200V1400Ω=17A
Step 4: Calculate the Voltage Drop Across Each Bulb
Now we can find the voltage drop across each bulb using Ohm's Law (V = IR).
For the 40 W bulb:
V1=I×R1=(17A)×(1000Ω)=10007V≈142.86V
For the 100 W bulb:
V2=I×R2=(17A)×(400Ω)=4007V≈57.14V
Step 5: Conclusion
The potential drop across the 40 W bulb is approximately 142.86 V, and the potential drop across the 100 W bulb is approximately 57.14 V. Therefore, the potential difference across the 40 W bulb is greater than that across the 100 W bulb.
Final Answer
The potential drop across the 40 W bulb is greater than that across the 100 W bulb.
---
We know the power (P) and voltage (V) for each bulb. The resistance (R) can be calculated using the formula:
R=V2P
R1=(200V)240W=4000040=1000Ω
R2=(200V)2100W=40000100=400Ω
Since the bulbs are connected in series, the total resistance (R_total) is the sum of the individual resistances:
Rtotal=R1+R2=1000Ω+400Ω=1400Ω
Using Ohm's Law, the current (I) in the circuit can be calculated using the total voltage (V_total) and the total resistance (R_total):
I=VtotalRtotal=200V1400Ω=17A
Now we can find the voltage drop across each bulb using Ohm's Law (V = IR).
V1=I×R1=(17A)×(1000Ω)=10007V≈142.86V
V2=I×R2=(17A)×(400Ω)=4007V≈57.14V
The potential drop across the 40 W bulb is approximately 142.86 V, and the potential drop across the 100 W bulb is approximately 57.14 V. Therefore, the potential difference across the 40 W bulb is greater than that across the 100 W bulb.
The potential drop across the 40 W bulb is greater than that across the 100 W bulb.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Three bulbs of 40W,60Wand100W are connected in series with a 240V source.
View SolutionTwo bulbs 100W,250V and 200W,250V are connected in parallel across a 500V line. Then-
View SolutionTwo 120 V light bulbs, one of 25 W other of 200 W were connected in series across a 240 V line. One bulb burnt out almost instantaneously. Which one was burnt and why ?
View SolutionTwo electic bulbs marked 25W−220V and 100W−220V are connected in series to a 440 V supply. Which of the bulbs will fuse?
View SolutionWhen three identical bulbs of 60W,200V rating are connected in series to a 200V supply, the power drawn by them will be
View SolutionIf two bulbs of 25 W and 100 W rated at 200 volts are connected in series across a 440 volts supply, then
View SolutionTwo electric bulbs , rated at (25W,220V) and (100W,220V), are connected in series across a 220 V voltage source , if the 25W and 100W bulbs draw powers P1andP2 Respectively , then :
View SolutionTwo bulbs are marked 220 V, 100 W and 220 V, 50W respectively. They are connected in series to 220 V mains. Find the ratio of heats generated in them.
View SolutionBulb B1(100W−250V) and bulb B2(100W−200V) are connected across 250V. What is potential drop across B2 ?
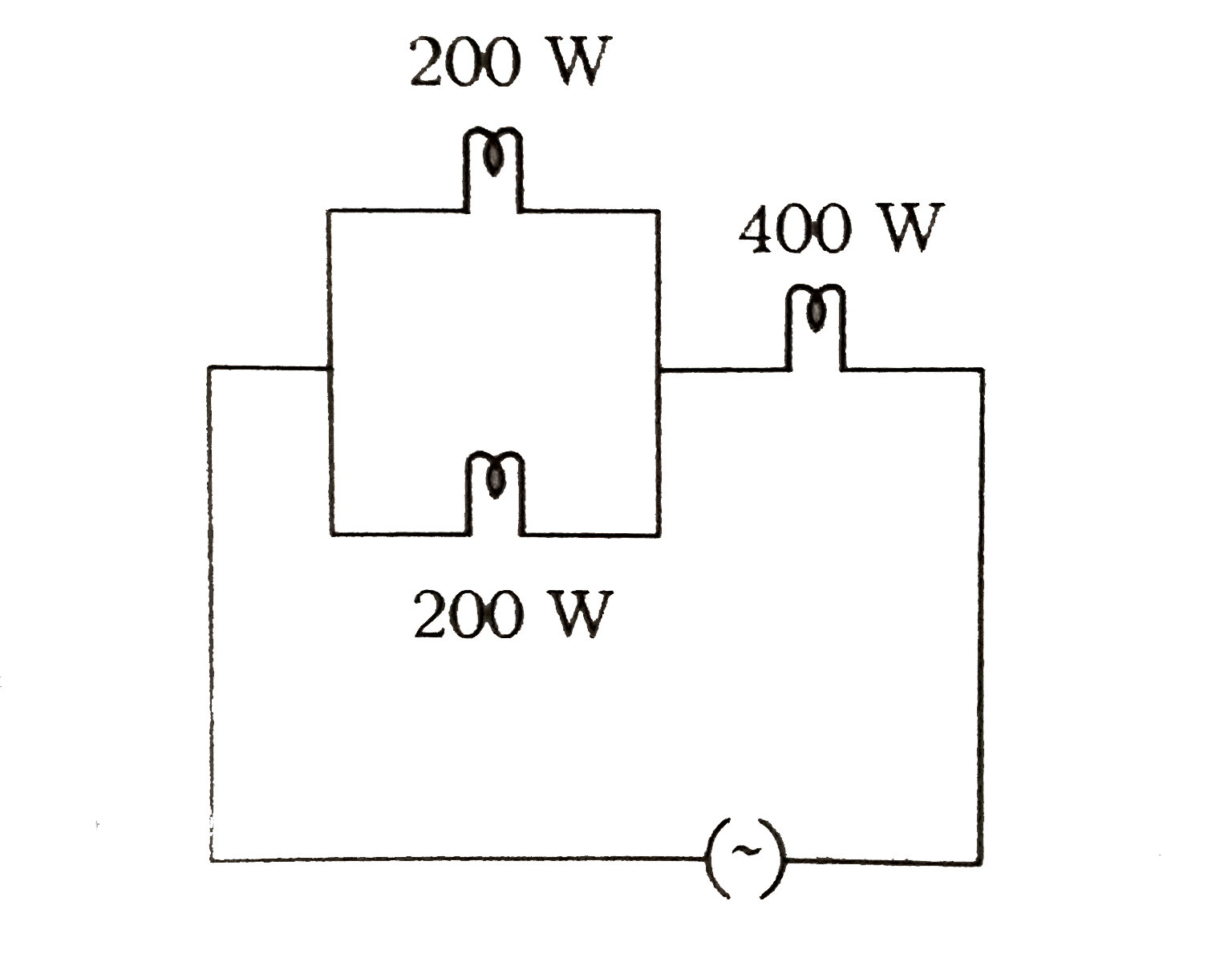
View SolutionThree electric bulbs of 200 W, 200 W and 400 W are connected as shown in figure. The resultant power of the combination is
View Solution
