24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
all cells are connected in series combination
all cells are connected in parallel combination
4 cells in each row are connected in series and 6 such rows are connected in parallel
6 cells in each row are connected in series and 4 such rows are connected in parallel
The correct Answer is:D
To solve the problem of determining the configuration of 24 cells that will yield the maximum current when connected to an external resistance of 1.5 ohms, we will analyze each of the proposed configurations step by step.
Step 1: Understanding the Problem
We have 24 cells, each with an EMF of 1.5 V and an internal resistance of 1 ohm. We need to determine the configuration that produces the maximum current when connected to an external resistance of 1.5 ohms.
Step 2: Configuration A - All Cells in Series
1. Calculate the Equivalent EMF (E_eq):
Eeq=n⋅e=24⋅1.5=36 V
2. Calculate the Equivalent Internal Resistance (R_eq):
Req=n⋅r=24⋅1=24 ohms
3. Calculate the Total Resistance (R_total):
Rtotal=Req+Rexternal=24+1.5=25.5 ohms
4. Calculate the Current (I):
I=EeqRtotal=3625.5≈1.41 A
Step 3: Configuration B - All Cells in Parallel
1. Calculate the Equivalent EMF (E_eq):
Eeq=e=1.5 V
2. Calculate the Equivalent Internal Resistance (R_eq):
Req=rn=124 ohms
3. Calculate the Total Resistance (R_total):
Rtotal=Req+Rexternal=124+1.5≈1.54 ohms
4. Calculate the Current (I):
I=EeqRtotal=1.51.54≈0.97 A
Step 4: Configuration C - 4 Cells in Series, 6 Rows in Parallel
1. Calculate the Equivalent EMF for each row (E_eq):
Eeq=4⋅1.5=6 V
2. Calculate the Equivalent Internal Resistance for each row (R_eq):
Req=4⋅1=4 ohms
3. Calculate the Total Equivalent Resistance (R_total):
Req_total=Reqn=46=23 ohms
Rtotal=Req_total+Rexternal=23+1.5=23+96=116 ohms
4. Calculate the Current (I):
I=EeqRtotal=6116=3611≈3.27 A
Step 5: Configuration D - 6 Cells in Series, 4 Rows in Parallel
1. Calculate the Equivalent EMF for each row (E_eq):
Eeq=6⋅1.5=9 V
2. Calculate the Equivalent Internal Resistance for each row (R_eq):
Req=6⋅1=6 ohms
3. Calculate the Total Equivalent Resistance (R_total):
Req_total=Reqn=64=1.5 ohms
Rtotal=Req_total+Rexternal=1.5+1.5=3 ohms
4. Calculate the Current (I):
I=EeqRtotal=93=3 A
Conclusion
After calculating the current for each configuration:
- Configuration A: 1.41 A
- Configuration B: 0.97 A
- Configuration C: 3.27 A
- Configuration D: 3 A
The maximum current is obtained in Configuration C (4 cells in series, 6 rows in parallel) with a current of approximately 3.27 A.
We have 24 cells, each with an EMF of 1.5 V and an internal resistance of 1 ohm. We need to determine the configuration that produces the maximum current when connected to an external resistance of 1.5 ohms.
1. Calculate the Equivalent EMF (E_eq):
Eeq=n⋅e=24⋅1.5=36 V
2. Calculate the Equivalent Internal Resistance (R_eq):
Req=n⋅r=24⋅1=24 ohms
Rtotal=Req+Rexternal=24+1.5=25.5 ohms
I=EeqRtotal=3625.5≈1.41 A
1. Calculate the Equivalent EMF (E_eq):
Eeq=e=1.5 V
Req=rn=124 ohms
Rtotal=Req+Rexternal=124+1.5≈1.54 ohms
I=EeqRtotal=1.51.54≈0.97 A
1. Calculate the Equivalent EMF for each row (E_eq):
Eeq=4⋅1.5=6 V
Req=4⋅1=4 ohms
Req_total=Reqn=46=23 ohms
Rtotal=Req_total+Rexternal=23+1.5=23+96=116 ohms
I=EeqRtotal=6116=3611≈3.27 A
1. Calculate the Equivalent EMF for each row (E_eq):
Eeq=6⋅1.5=9 V
Req=6⋅1=6 ohms
Req_total=Reqn=64=1.5 ohms
Rtotal=Req_total+Rexternal=1.5+1.5=3 ohms
I=EeqRtotal=93=3 A
After calculating the current for each configuration:
- Configuration A: 1.41 A
- Configuration B: 0.97 A
- Configuration C: 3.27 A
- Configuration D: 3 A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThe diagram in Fig. shows a cell of e.m.f. ε=2 volt and internal resistance r = 1 ohm connected to an external resistance R = 4 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
the key K is closed.

View SolutionThe diagram in Fig. shows a cell of e.m.f. ε=2 volt and internal resistance r = 1 ohm connected to an external resistance R = 4 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
the key K is open

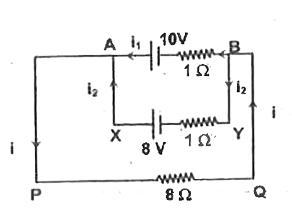
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionA battery has e.m.f. 4 V and internal resistance r . When this battery is connected to an external resistance of 2 ohms , a current of 1 amp . flows in the circuit. How much current will flow if the terminals of the battery are connected directly
View SolutionA cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
View SolutionA student is asked to connected four cells of e.m.f of 1 V and internal resistance 0.5 ohm in series with a external resistance of 1 ohm. But one cell is wrongly connected by him with its terminal reversed, the current in the circuit is
View SolutionTwo batteries (connected in series) of same emf 10 V of internal resistances 20ohm and 5ohm are connected to a load resistance of 30ohm. Now an unknown resistance x is connected in parallel to the load resistance. Find value of x so that potential drop of battery having internal resistance 20ohm becomes zero.
View SolutionA battery is designed by connecting four cells, each of emf 1.5 V and resistance 2.0 ohm in parallel. If this battery is now connected to an resistance of 2.5 ohm, find
the current flowing in the external circuit
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View Solution
