A wire, carriying a current I is kept in the x-y plame the curve y -(2 cm) x=lambda//2
To find the magnitude of the magnetic force on the portion of the wire between z=0 and x=λ2, we can follow these steps:
Step 1: Understand the Configuration
The wire carries a current I and is located in the x-y plane along the curve y=2cmsin(2πλx). The magnetic field B is directed along the z-axis.
Step 2: Identify the Force Formula
The magnetic force F on a current-carrying wire in a magnetic field is given by:
F=I∫dl×B
where dl is a differential length element of the wire and B is the magnetic field vector.
Step 3: Determine the Differential Length Element
Since the wire follows a curve, we need to express dl in terms of dx and dy. The differential length element can be expressed as:
dl=dx^i+dy^j
where dy=dydxdx.
Step 4: Calculate dydx
From the equation of the curve:
y=2cmsin(2πλx)
Differentiating y with respect to x:
dydx=2cm⋅2πλcos(2πλx)
Step 5: Set up the Integral for Force
The force can be calculated as:
F=I∫λ20dl×B
Since B is in the z-direction, we can write:
B=B^k
Thus, the cross product dl×B becomes:
dl×B=(dx^i+dy^j)×(B^k)=B(dy^i−dx^j)
Step 6: Substitute and Integrate
Substituting dy into the integral:
F=I∫λ20B(2cm⋅2πλcos(2πλx)dx^i−dx^j)
This integral can be separated into two parts, one for ^i and one for ^j.
Step 7: Calculate the Magnitude of the Force
The total force will be the sum of the components from the two integrals. The limits of integration are from 0 to λ2.
Final Expression for the Force
After evaluating the integrals, we will find the magnitude of the force F. The final expression will depend on the constants I, B, and λ.
The wire carries a current I and is located in the x-y plane along the curve y=2cmsin(2πλx). The magnetic field B is directed along the z-axis.
The magnetic force F on a current-carrying wire in a magnetic field is given by:
F=I∫dl×B
where dl is a differential length element of the wire and B is the magnetic field vector.
Since the wire follows a curve, we need to express dl in terms of dx and dy. The differential length element can be expressed as:
dl=dx^i+dy^j
where dy=dydxdx.
From the equation of the curve:
y=2cmsin(2πλx)
Differentiating y with respect to x:
dydx=2cm⋅2πλcos(2πλx)
The force can be calculated as:
F=I∫λ20dl×B
Since B is in the z-direction, we can write:
B=B^k
Thus, the cross product dl×B becomes:
dl×B=(dx^i+dy^j)×(B^k)=B(dy^i−dx^j)
Substituting dy into the integral:
F=I∫λ20B(2cm⋅2πλcos(2πλx)dx^i−dx^j)
This integral can be separated into two parts, one for ^i and one for ^j.
The total force will be the sum of the components from the two integrals. The limits of integration are from 0 to λ2.
After evaluating the integrals, we will find the magnitude of the force F. The final expression will depend on the constants I, B, and λ.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A wire, carrying a current i, is kept in the x−y plane along the curve y=Asin(2πλx). A magnetic field B exists in the z-direction. Find the magnitude of the magnetic force on the portion of the wire between x=0andx=λ.
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View Solution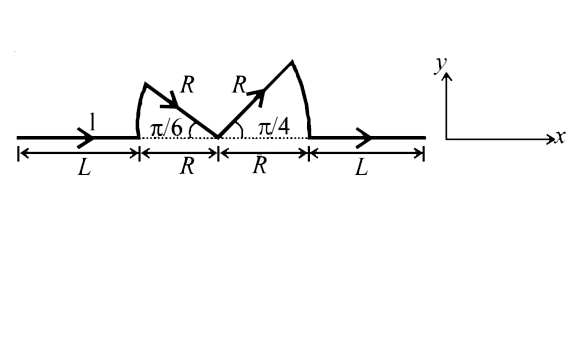
A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic field B. If F is the magnitude of the total magnetic force acting on the conductor, then the correct statement is/are
View SolutionA conductor (shown in the figure) carrying constant current I is kept in the x−y plane in a uniform magnetic field →B. If →F is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)

View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire carrying a current i is placed in a uniform magnetic field in the form of the curve y=asin(πxL)0≤x≤2L. The force acting on the wire is
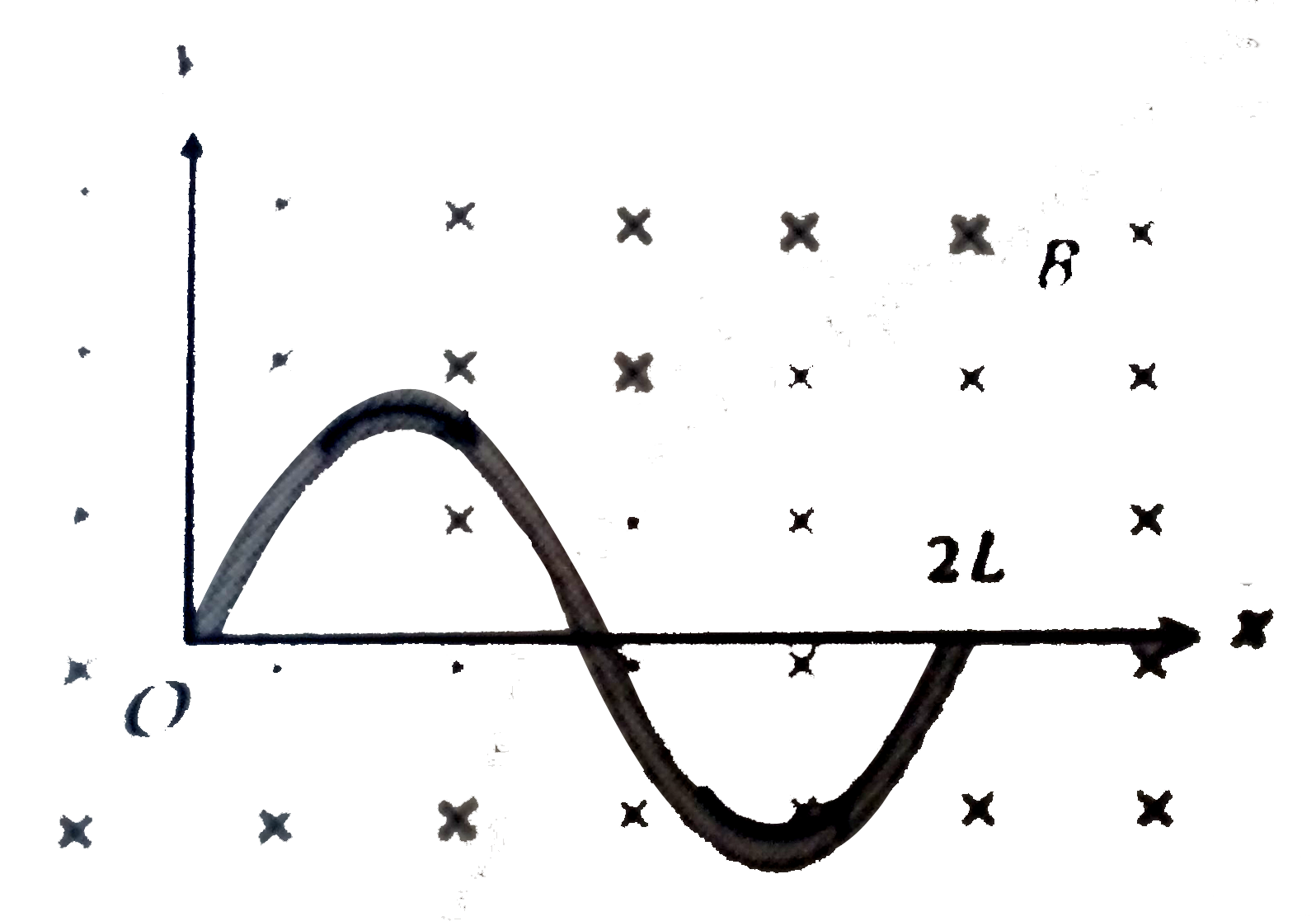
View SolutionA current of 5.0 A exists in the circuit shown in The wire PQ has a length of 50 cm the magnetic field in which it is immersed has a magnitude of 0.20 T. Find the magnetic force acting on the wire PQ.

View Solution
A current of 10A exists in the circuit figure.The wire PQ has a lengths of 100cm and the magnetic field in which it is immersed has a magnitude of 0.20T.Find the magnetic force acting on the wire PQ.
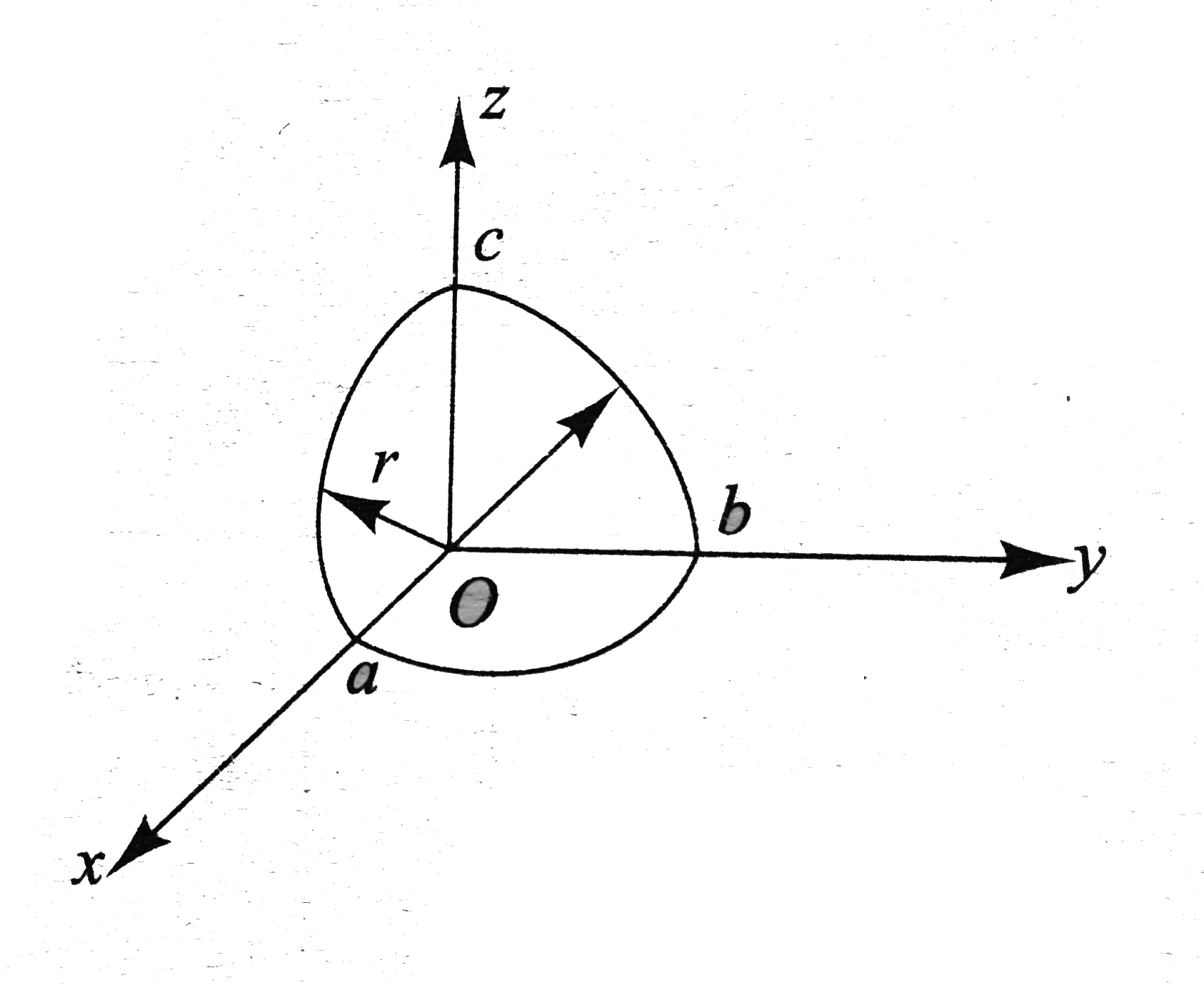
View SolutionA wire is bent into three circular segment of radius r=10cm as shown in. Each segment is a quadrant of a circle ab lying in the x−y plane, bc lying in the y−z plane and ca lying in the z−x plane.
(a) if a magnetic field B points in the positive x direction, what is the magnitude of the emf developed in the wire when B increases at the rate of 3mTs−1?
(b) What is the direction of teh current in the segment bc.
View Solution
