Two electrons move parallel to each other with equal speed 'V' the ratio of magnetic & electric force between them is
To solve the problem of finding the ratio of magnetic force to electric force between two electrons moving parallel to each other with equal speed V, we can follow these steps:
Step 1: Determine the Electric Force
The electric force Fe between two electrons can be calculated using Coulomb's law. The formula is given by:
Fe=14πϵ0⋅e2r2
where:
- e is the charge of an electron,
- r is the distance between the two electrons,
- ϵ0 is the permittivity of free space.
Step 2: Determine the Magnetic Field
Next, we need to find the magnetic field B created by one electron at the position of the other. The magnetic field due to a moving charge can be calculated using the Biot-Savart law. For an electron moving with speed V, the magnetic field at a distance r is given by:
B=μ04π⋅I⋅dLr2
where:
- I is the current equivalent to the moving charge,
- dL is the differential length element (considered as 1 for simplicity).
For an electron, the current I can be expressed as:
I=eT=erV=eVr
Substituting this into the magnetic field equation gives:
B=μ04π⋅eVr2
Step 3: Calculate the Magnetic Force
The magnetic force Fm on one electron due to the magnetic field created by the other electron is given by:
Fm=e⋅V⋅B
Substituting the expression for B:
Fm=e⋅V⋅(μ04π⋅eVr2)
This simplifies to:
Fm=μ0e2V24πr2
Step 4: Find the Ratio of Magnetic Force to Electric Force
Now we can find the ratio of the magnetic force to the electric force:
FmFe=μ0e2V24πr214πϵ0⋅e2r2
This simplifies to:
FmFe=μ0V21ϵ0=μ0ϵ0V2
Step 5: Use the Relationship Between μ0, ϵ0, and c
From electromagnetic theory, we know that:
μ0ϵ0=1c2
where c is the speed of light. Therefore, we can substitute this into our ratio:
FmFe=V2c2
Final Answer
Thus, the ratio of the magnetic force to the electric force between the two electrons is:
FmFe=V2c2
The electric force Fe between two electrons can be calculated using Coulomb's law. The formula is given by:
- e is the charge of an electron,
- r is the distance between the two electrons,
- ϵ0 is the permittivity of free space.
Next, we need to find the magnetic field B created by one electron at the position of the other. The magnetic field due to a moving charge can be calculated using the Biot-Savart law. For an electron moving with speed V, the magnetic field at a distance r is given by:
- I is the current equivalent to the moving charge,
- dL is the differential length element (considered as 1 for simplicity).
The magnetic force Fm on one electron due to the magnetic field created by the other electron is given by:
Now we can find the ratio of the magnetic force to the electric force:
From electromagnetic theory, we know that:
Thus, the ratio of the magnetic force to the electric force between the two electrons is:
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
If two protons are moving with speed v=4.5×105m/s parallel to each other then find the ratio of electrostatic and magnetic force between them : -
View SolutionTwo protons move parallel to each other with an equal velocity v=300kms−1. Find the ratio of forces of magnetic and electric interaction of the protons.
View SolutionTwo streams of electrons are moving parallel to each other in the same direction. They
View SolutionWhen the two plane mirror are parallel to each other, then the number of images of an object placed between them is
View SolutionIf two steams of proton move parallel to each other in the same direction, then they
View SolutionTwo infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
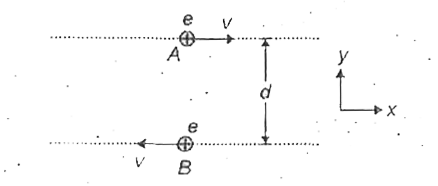
View SolutionTwo protons A and B move parallel to the x-axis is opposite directions with equal speed v. At the instant shown, the ratio of magnetic force and electric force acting on the proton A is (c=speed of light in vacuum)
View SolutionFind the ratio of the electric and gravitational forces between two protons.
View SolutionThe object at rest suddenly explodes into three parts with the mass ratio 2:1:1. The parts of equal masses move at right angles to each other with equal speeds. What is the speed of the third part after the explosion?
View SolutionCalculate the ratio of electric to gravitational force between two electrons.
View Solution
