Two infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
To solve the problem of finding the intensity of the electric field at a point midway between two infinitely long straight wires with uniform linear charge densities λ and 2λ, we can follow these steps:
1. Identify the Setup:
- We have two infinitely long straight wires parallel to each other.
- The distance between the wires is r.
- The linear charge density of the first wire is λ and that of the second wire is 2λ.
2. Determine the Midpoint:
- The point of interest is midway between the two wires. This point is at a distance of r2 from each wire.
3. Electric Field Due to a Long Charged Wire:
- The electric field E due to an infinitely long straight wire with linear charge density λ at a distance d from the wire is given by:
E=λ2πϵ0d
- Here, ϵ0 is the permittivity of free space.
4. Calculate the Electric Field from Each Wire:
- For the first wire (charge density λ):
E1=λ2πϵ0(r2)=2λπϵ0r
- For the second wire (charge density 2λ):
E2=2λ2πϵ0(r2)=4λπϵ0r
5. Direction of the Electric Fields:
- The electric field due to the first wire (with charge density λ) points away from the wire.
- The electric field due to the second wire (with charge density 2λ) also points away from the wire.
- Since the wires are parallel, the electric fields will point in opposite directions at the midpoint.
6. Net Electric Field Calculation:
- The net electric field Enet at the midpoint is the difference between the two electric fields:
Enet=E2−E1
- Substituting the values:
Enet=4λπϵ0r−2λπϵ0r=2λπϵ0r
7. Final Result:
- Therefore, the intensity of the electric field at the point midway between the two wires is:
Enet=2λπϵ0r
- We have two infinitely long straight wires parallel to each other.
- The distance between the wires is r.
- The linear charge density of the first wire is λ and that of the second wire is 2λ.
- The point of interest is midway between the two wires. This point is at a distance of r2 from each wire.
- The electric field E due to an infinitely long straight wire with linear charge density λ at a distance d from the wire is given by:
E=λ2πϵ0d
- Here, ϵ0 is the permittivity of free space.
- For the first wire (charge density λ):
E1=λ2πϵ0(r2)=2λπϵ0r
- For the second wire (charge density 2λ):
E2=2λ2πϵ0(r2)=4λπϵ0r
- The electric field due to the first wire (with charge density λ) points away from the wire.
- The electric field due to the second wire (with charge density 2λ) also points away from the wire.
- Since the wires are parallel, the electric fields will point in opposite directions at the midpoint.
- The net electric field Enet at the midpoint is the difference between the two electric fields:
Enet=E2−E1
- Substituting the values:
Enet=4λπϵ0r−2λπϵ0r=2λπϵ0r
- Therefore, the intensity of the electric field at the point midway between the two wires is:
Enet=2λπϵ0r
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXAMPLE138videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE20videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-I Subjective Type Questions6videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)15videos
GRAVITATION
Similar Questions
Two parallel infinite line charges +λand−λ are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View SolutionBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :
 View Solution
View SolutionAn infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
View SolutionAn infinitely long thin straight wire has uniform linear charge density of 1/4 coul m−1. Then the magnitude of the electric intensity at a point 18 cm away is
View SolutionTwo infinitely long parallel wires having linear charge densities λ1 and λ2 respectively are placed at a distance of R metres. The force per unit length on either wire will be (k=14πε0)
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
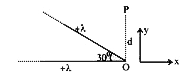 View Solution
View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:
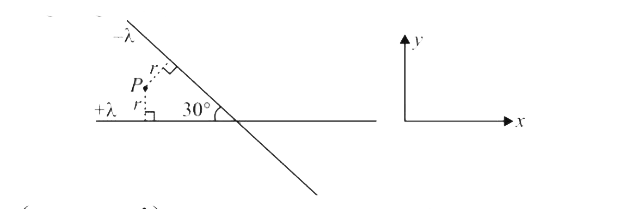 View Solution
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:
 View Solution
View Solution

