A current of 0.5 A is passed through the coil of a galvanometer having 500 turns and each turns has an average area of 3×10−4m2 if a torque of 1.5 N-m is required for this coil carrying same current to set it parallel to a magnetic field calculate the strength of the magnetic field
To solve the problem step by step, we will use the formula for torque in a magnetic field and the definition of magnetic moment.
Step 1: Understand the formula for torque
The torque (τ) experienced by a coil in a magnetic field is given by the formula:
τ=n⋅I⋅A⋅B
where:
- n = number of turns in the coil
- I = current through the coil
- A = area of each turn of the coil
- B = magnetic field strength
Step 2: Rearrange the formula to solve for magnetic field strength
We need to find the magnetic field strength (B). Rearranging the formula gives us:
B=τn⋅I⋅A
Step 3: Substitute the given values into the formula
From the problem, we have:
- τ=1.5N-m
- n=500 turns
- I=0.5A
- A=3×10−4m2
Now substituting these values into the formula:
B=1.5500⋅0.5⋅(3×10−4)
Step 4: Calculate the denominator
Calculating the denominator:
500⋅0.5=250
250⋅(3×10−4)=250⋅3⋅10−4=750×10−4=7.5×10−2
Step 5: Calculate the magnetic field strength
Now substituting back into the equation for B:
B=1.57.5×10−2=1.50.075=20T
Final Answer
The strength of the magnetic field is:
B=20T
---
The torque (τ) experienced by a coil in a magnetic field is given by the formula:
τ=n⋅I⋅A⋅B
where:
- n = number of turns in the coil
- I = current through the coil
- A = area of each turn of the coil
- B = magnetic field strength
We need to find the magnetic field strength (B). Rearranging the formula gives us:
B=τn⋅I⋅A
From the problem, we have:
- τ=1.5N-m
- n=500 turns
- I=0.5A
- A=3×10−4m2
B=1.5500⋅0.5⋅(3×10−4)
Calculating the denominator:
500⋅0.5=250
250⋅(3×10−4)=250⋅3⋅10−4=750×10−4=7.5×10−2
Now substituting back into the equation for B:
B=1.57.5×10−2=1.50.075=20T
The strength of the magnetic field is:
B=20T
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
Similar Questions
A conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View SolutionA circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View Solution
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A circular coil having N turns and radius r carries a current I. It is held in the XZ plane in a magnetic field Bˆi. The torque on the coil due to the magnetic field is :
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
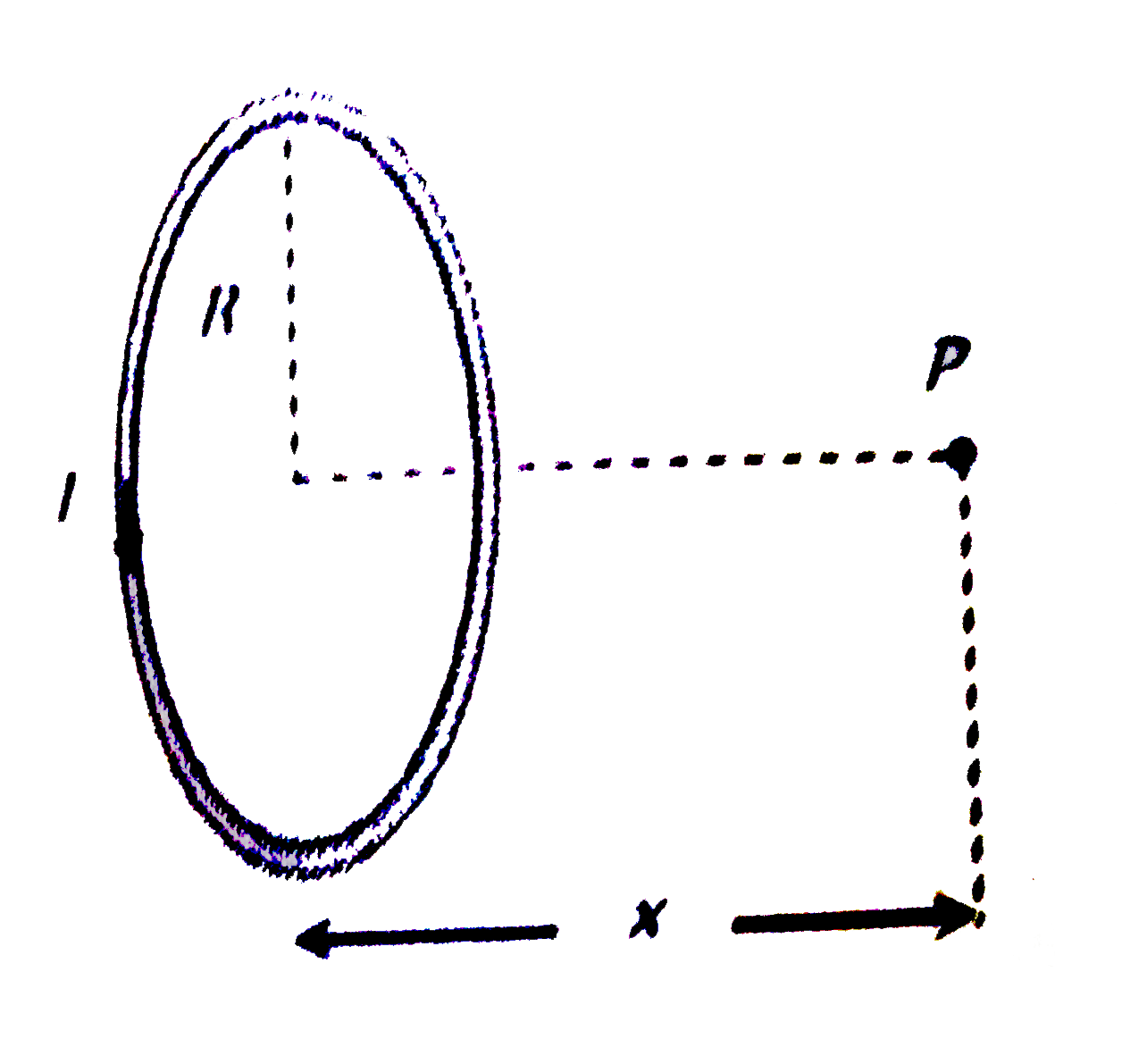
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
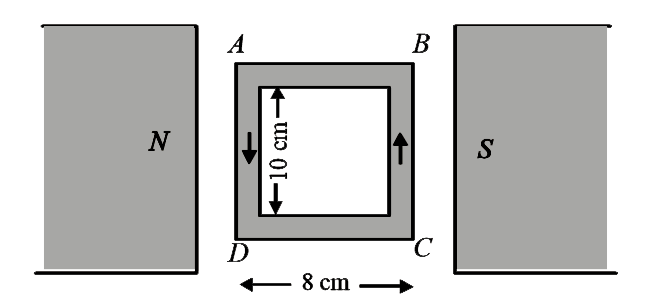
View SolutionA 100 turns coil shown in figure carries a current of 2 amp in a magnetic field B=0.2Wb/m2. The torque acting on the coil is
View SolutionA moving coil galvanometer has 100 turns and each turn has an area 2.0cm2. The magnetic field produced by the magnet is 0.01T. The deflection in the coil is 0.05 radian when a current of 10mA is passed through it. Find the torsional constant of the suspension wire.
View SolutionA moving coil galvanometer has 100 turns and each turn has an area 2.0cm2. The magnetic field produced by the magnet is 0.01T. The deflection in the coil is 0.05 radian when a current of 10mA is passed through it. Find the torsional constant of the suspension wire.
View Solution