In using Ampere's law,to find the magnetic field inside a straight long soleniod the loop that is taken is
A circular loop in a with the soleniod
a rectangular loop in a plane is perpendicular to the axis of the solenoid
A rectangulr loop in a plane containing the axis of the solenoid the loop being totally within the soleniod
A rectangular loop in a plane containing the axis of the soleniod the loop being partly inside and partly outside it
The correct Answer is:D
To solve the question regarding the application of Ampere's law to find the magnetic field inside a straight long solenoid, we will analyze the options provided and determine which loop is appropriate for our calculations.
1. Understanding Ampere's Law:
Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I passing through the loop. Mathematically, it is expressed as:
∮B⋅dl=μ0Ienc
2. Analyzing the Options:
We have four options regarding the type of loop we can use to apply Ampere's law in the context of a solenoid.
- Option A: A circular loop with the solenoid.
- Option B: A rectangular loop in a plane perpendicular to the axis of the solenoid.
- Option C: A rectangular loop in a plane containing the axis of the solenoid, the loop being totally within the solenoid.
- Option D: A rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
3. Evaluating Each Option:
- Option A: A circular loop is not suitable because it does not align well with the uniform magnetic field inside the solenoid.
- Option B: A rectangular loop perpendicular to the axis of the solenoid results in B⋅dl=0 since the angle θ between B and dl is 90 degrees, leading to no contribution to the integral.
- Option C: A rectangular loop totally within the solenoid would not allow us to measure the current effectively since the magnetic field lines are uniform and parallel to the axis of the solenoid.
- Option D: A rectangular loop that is partially inside and partially outside the solenoid allows us to utilize Ampere's law effectively. The segment of the loop inside the solenoid will experience the magnetic field, while the segments outside will not contribute to the integral.
4. Conclusion:
The best choice for applying Ampere's law to find the magnetic field inside a straight long solenoid is Option D: a rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
Final Answer:
Option D: A rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I passing through the loop. Mathematically, it is expressed as:
∮B⋅dl=μ0Ienc
We have four options regarding the type of loop we can use to apply Ampere's law in the context of a solenoid.
- Option B: A rectangular loop in a plane perpendicular to the axis of the solenoid.
- Option C: A rectangular loop in a plane containing the axis of the solenoid, the loop being totally within the solenoid.
- Option D: A rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
- Option A: A circular loop is not suitable because it does not align well with the uniform magnetic field inside the solenoid.
- Option B: A rectangular loop perpendicular to the axis of the solenoid results in B⋅dl=0 since the angle θ between B and dl is 90 degrees, leading to no contribution to the integral.
- Option C: A rectangular loop totally within the solenoid would not allow us to measure the current effectively since the magnetic field lines are uniform and parallel to the axis of the solenoid.
- Option D: A rectangular loop that is partially inside and partially outside the solenoid allows us to utilize Ampere's law effectively. The segment of the loop inside the solenoid will experience the magnetic field, while the segments outside will not contribute to the integral.
The best choice for applying Ampere's law to find the magnetic field inside a straight long solenoid is Option D: a rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
Option D: A rectangular loop in a plane containing the axis of the solenoid, the loop being partially inside and partially outside.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
Similar Questions
The magnetic field inside a solenoid is-
View SolutionThe magnetic field lines inside a bar magnet
View SolutionA current loop in a magnetic field
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
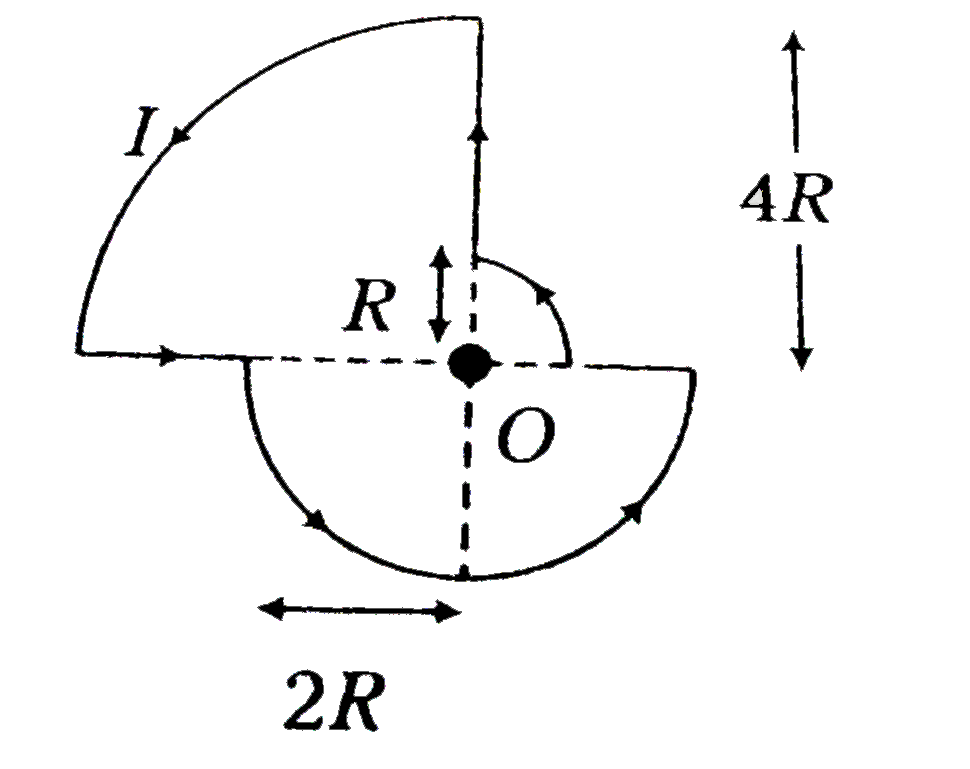
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
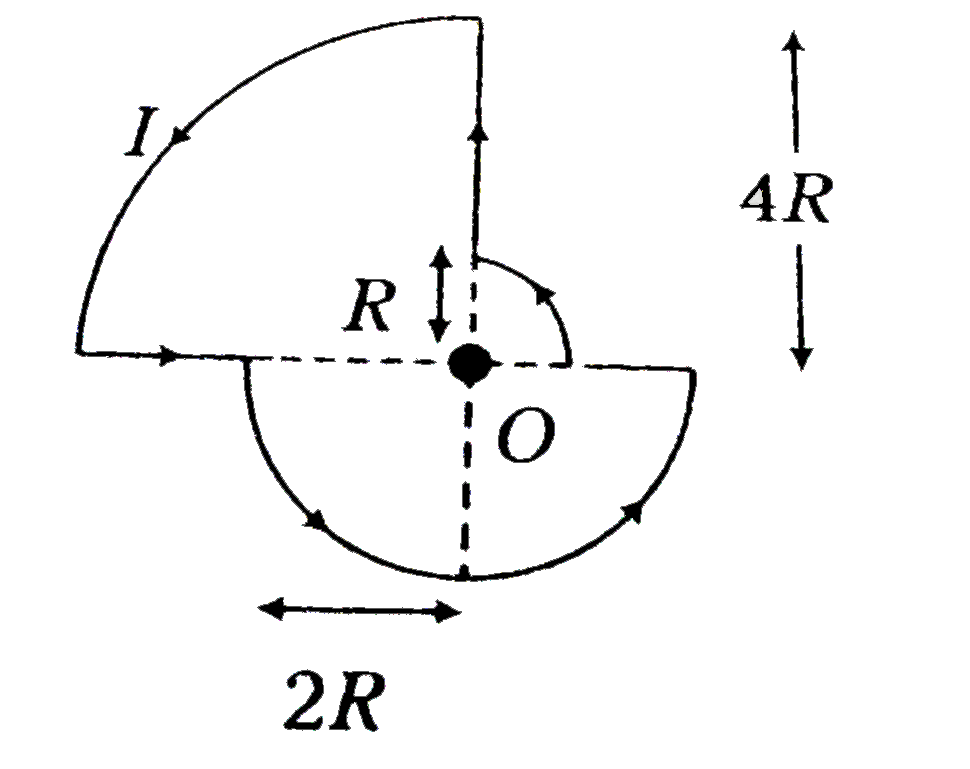
View Solution(a)Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b )How is the magnetic field inside a given solenoid made strong?
View SolutionCan you use Ampere's law of find the magnetic field at the centre of a ring of radius R and carrying current l?
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionIn order to have a current in a long wire, it should be
connected to a battery or some such device. Can we
obtain the magnetic field due to a straight, long wire by
using Ampere's law without mentioning this other part of the circuit?
View SolutionWith the help of a labelled circuit diagram, illustrate the pattern of field lines of the magnetic field around a current-carrying straight long conducting wire. How is the right hand thumb rule useful to find direction of magnetic field associated with a current-carrying conductor?
View Solution
