In order to have a current in a long wire, it should be
connected to a battery or some such device. Can we
obtain the magnetic field due to a straight, long wire by
using Ampere's law without mentioning this other part of the circuit?
To solve the question step by step, we will break it down into two parts as presented in the video transcript.
Step 1: Understanding the Requirement for Current Flow
1. Current Flow in a Wire: To have a current flowing in a long wire, it must be connected to a power source, such as a battery. This is essential because the battery provides the necessary potential difference that drives the electrons through the wire, creating a current.
- Conclusion: Yes, a long wire must be connected to a battery or some other device to have current flow.
1. Current Flow in a Wire: To have a current flowing in a long wire, it must be connected to a power source, such as a battery. This is essential because the battery provides the necessary potential difference that drives the electrons through the wire, creating a current.
- Conclusion: Yes, a long wire must be connected to a battery or some other device to have current flow.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
In using Ampere's law,to find the magnetic field inside a straight long soleniod the loop that is taken is
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionConsider a 10-cm long piece of a wire which carries a current of 10A . Find the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.
View SolutionStatement-1: Ampere's law cannot be used determine magnetic field due a current carrying wire of finite length
Statement-2: Ampere's law is not valid for wires finite length
View SolutionA very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
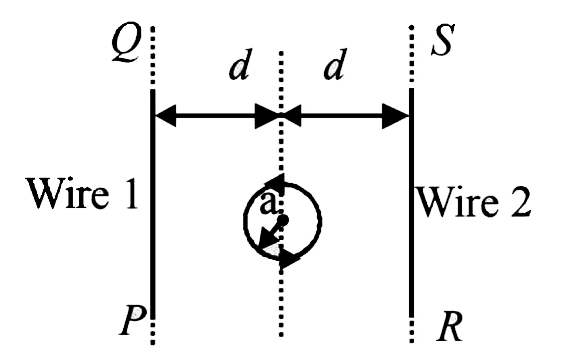
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that case
View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution
