A charged particle is rotating in uniform circular motion in a uniform magnetic field . Let r= radius of circule, v= speed of particle k = kinetic energy, a= magnitude of acceleration , p= magnitude of linear momentum, =specific charge and angular speed. then match the following two columns.

The correct Answer is:
Step by step video & image solution for A charged particle is rotating in uniform circular motion in a uniform magnetic field . Let r= radius of circule, v= speed of particle k = kinetic energy, a= magnitude of acceleration , p= magnitude of linear momentum, q/m = alpha=specific charge and omega= angular speed. then match the following two columns. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A charged particle is moving in a circular path in uniform magnetic field. Match the following.

View SolutionA charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View SolutionAssertion A charged particle is rotating in a circular path in uniform magnetic field. Then, plane of circle is perpendicular to the magnetic field.
Reason Circular motion is a two-dimensional motion.
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA positively charged particle of charge 'q' enters in a uniform magnetic field B directed inward and is deflected a distance x after travelling a distance Y as shown in the figure. The magnitude of linear momentum of the particle is:
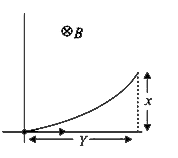
View SolutionA charged particle enters in a uniform magnetic field perpendicular to it. Now match the following two columns.

View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle is E, then frequency of rotation is
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
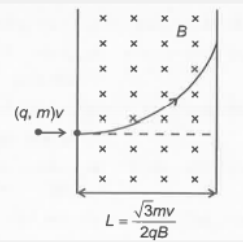
View Solution
