A charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle is E, then frequency of rotation is
qBmπ
qB2πm
qBE2πm
qB2πE
The correct Answer is:b
To solve the problem, we need to find the frequency of rotation of a charged particle with charge q and mass m that enters a magnetic field B perpendicularly, given that its kinetic energy is E.
1. Understanding the Kinetic Energy:
The kinetic energy E of the charged particle is given by the formula:
E=12mv2
where v is the velocity of the particle.
2. Relating Kinetic Energy to Velocity:
From the kinetic energy equation, we can express the velocity v in terms of kinetic energy E:
v=√2Em
3. Magnetic Force and Circular Motion:
When the charged particle moves in a magnetic field perpendicularly, it experiences a magnetic force that acts as the centripetal force required for circular motion. The magnetic force is given by:
F=qvB
The centripetal force needed for circular motion is given by:
Fc=mv2r
where r is the radius of the circular path.
4. Setting the Forces Equal:
Since the magnetic force provides the centripetal force, we can set these two forces equal:
qvB=mv2r
5. Solving for the Radius:
Rearranging the equation gives us:
r=mvqB
6. Finding Angular Frequency:
The angular frequency ω of the particle in circular motion is related to the velocity and radius by:
ω=vr
Substituting r from the previous step:
ω=vmvqB=qBm
7. Finding Frequency:
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting ω:
f=qB2πm
Final Answer:
Thus, the frequency of rotation of the charged particle is:
f=qB2πm
The kinetic energy E of the charged particle is given by the formula:
E=12mv2
where v is the velocity of the particle.
From the kinetic energy equation, we can express the velocity v in terms of kinetic energy E:
v=√2Em
When the charged particle moves in a magnetic field perpendicularly, it experiences a magnetic force that acts as the centripetal force required for circular motion. The magnetic force is given by:
F=qvB
The centripetal force needed for circular motion is given by:
Fc=mv2r
where r is the radius of the circular path.
Since the magnetic force provides the centripetal force, we can set these two forces equal:
qvB=mv2r
Rearranging the equation gives us:
r=mvqB
The angular frequency ω of the particle in circular motion is related to the velocity and radius by:
ω=vr
Substituting r from the previous step:
ω=vmvqB=qBm
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting ω:
f=qB2πm
Thus, the frequency of rotation of the charged particle is:
f=qB2πm
Similar Questions
If a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionFour charged particles are projected perpendicularly into the magnetic field with equal velocity. Which will have minimum frequency of rotation?
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60∘ with the boundary surface of magnetic field and comes out at an angle of 30∘ with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.

View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if
(a) d>muqB
(b) d<muqB
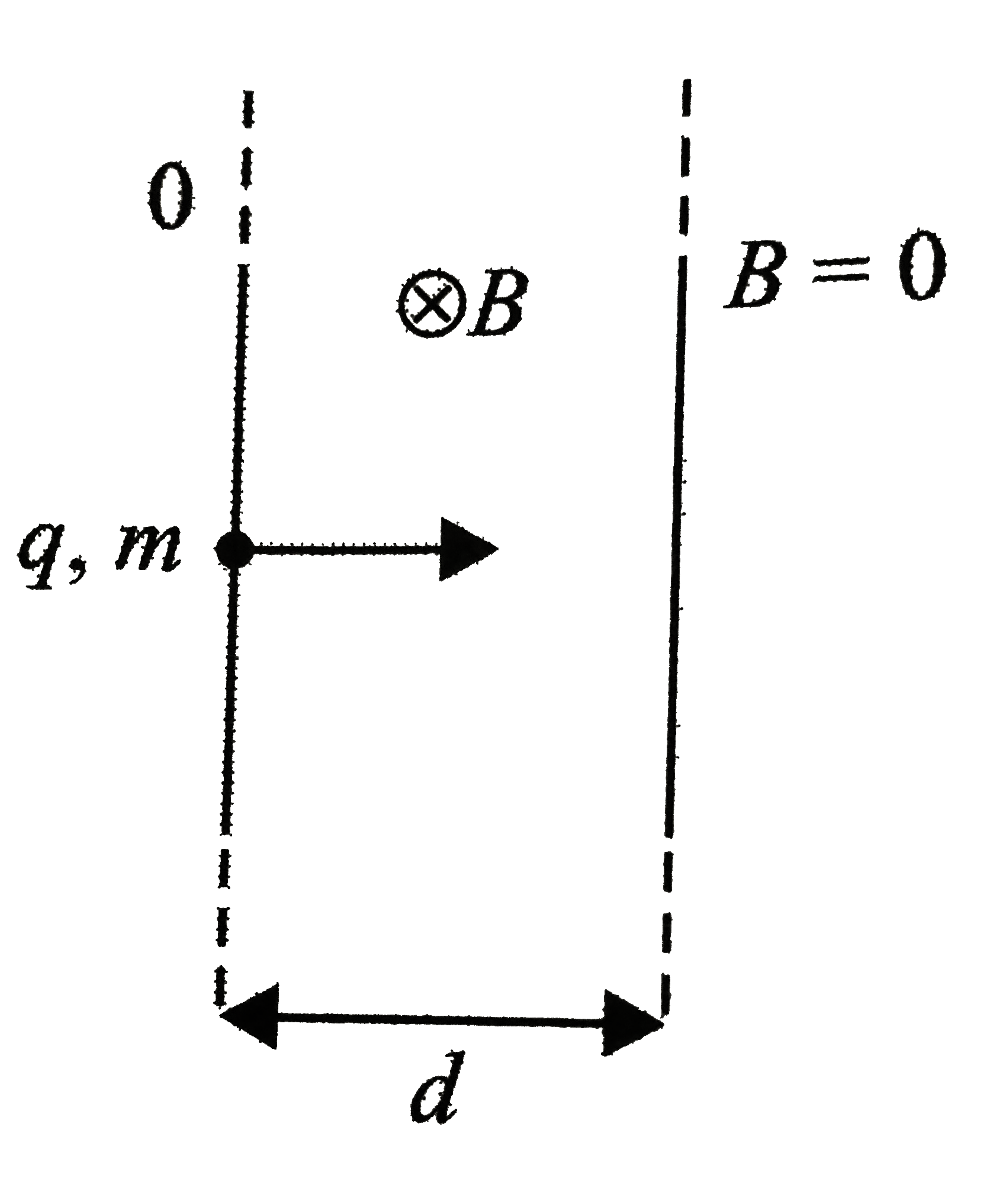
View SolutionA uniform mangetic field of strength B exists in a region of width d. A particle of charge q and mass m is shot perpendicularly (as shown in Fig. ) into the magnetic field. Find the time spent by the particle in the magnetic field if
(a) d>muqB
(b) d<muqB

View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be
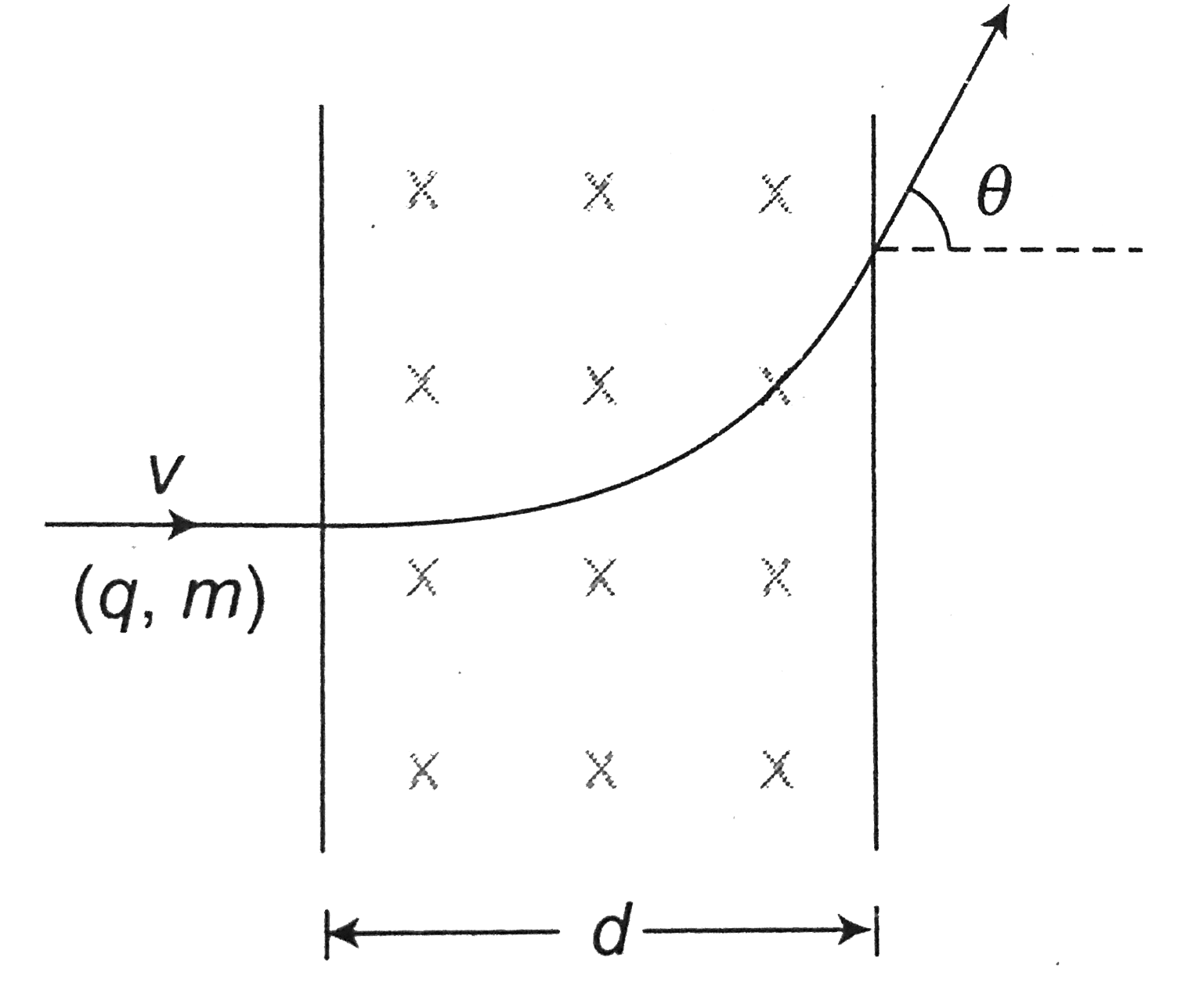
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View Solution
