When proton of KE = 1.0 MeV moving in South to North direction enters the magnetic field (from West to East direction), it accelerates with . The magnitude of magnetic field is-
0.71mT
71mT
7.1mT
0.071mT
The correct Answer is:1
To solve the problem, we will follow these steps:
Step 1: Convert Kinetic Energy to Joules
The kinetic energy (KE) of the proton is given as 1.0 MeV. We need to convert this to joules.
1 MeV=1.6×10−13 J
Step 2: Calculate the Velocity of the Proton
The kinetic energy of the proton can be expressed using the formula:
KE=12mv2
Where:
- KE=1.6×10−13 J
- m (mass of the proton) =1.67×10−27 kg
Rearranging the formula to find v:
v2=2×KEm
Substituting the values:
v2=2×1.6×10−131.67×10−27
Calculating v2:
v2=3.2×10−131.67×10−27≈1.916×1014
Taking the square root to find v:
v≈√1.916×1014≈1.38×107 m/s
Step 3: Use the Formula for Magnetic Force
The magnetic force acting on the proton can be expressed as:
F=qvB
Where:
- q (charge of the proton) =1.6×10−19 C
- a (acceleration) =1012 m/s2
From Newton's second law, we know:
F=ma
Setting the two expressions for force equal to each other:
ma=qvB
Step 4: Solve for the Magnetic Field B
Rearranging the equation to solve for B:
B=maqv
Substituting the known values:
B=(1.67×10−27 kg)(1012 m/s2)(1.6×10−19 C)(1.38×107 m/s)
Calculating B:
B≈1.67×10−152.208×10−12≈0.000757 T=0.757 mT
Step 5: Convert to milliTesla
Converting to milliTesla:
B≈0.757 mT≈0.71 mT
Final Answer
The magnitude of the magnetic field is approximately:
B≈0.71 mT
---
The kinetic energy (KE) of the proton is given as 1.0 MeV. We need to convert this to joules.
The kinetic energy of the proton can be expressed using the formula:
- KE=1.6×10−13 J
- m (mass of the proton) =1.67×10−27 kg
The magnetic force acting on the proton can be expressed as:
- q (charge of the proton) =1.6×10−19 C
- a (acceleration) =1012 m/s2
Rearranging the equation to solve for B:
Converting to milliTesla:
The magnitude of the magnetic field is approximately:
Topper's Solved these Questions
Similar Questions
In the given figure, the electron enters into the magnetic field. It deflects in ...... .. direction .
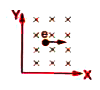
View SolutionAn electron moving towards the east enters a magnetic field directed towards the north. The force on the electron will be directed
View SolutionAn electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionA square loop of side 10cm and resistance 0.5Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70s at a steady rate. The magnitude of current in this time-interval is.
View SolutionA coil of 100 turns and area 2×10−2m2, pivoted about a vertical diameter in a uniform magnetic field carries a current of 5A. When the coil is held with its plane in North-South direction, it experiences a torque of 0.3N/m. When the plane is in East-West direction the torque is 0.4Nm. The value of magnetic induction is (Neglect earth's magnetic field)
View SolutionA charge +Q is moving upwards vertically. It enters a magnetic field directed to the north. The force on the charge will be towards
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionAn electron is moving vertically upwards in the uniform magnetic field of the earth. The velocity of the electron is 2.0×106 m/s and the horizontal component of the earth.s magnetic field is 0.32×10−4T. Obtain the magnitude and direction of the force on the electron.
View SolutionAn electron accelerated by a potential difference 2.5 kV moves horizontally into a region of space in which there is a downward directed uniform electric field of magnitude 10kVm−1.
(a) In what direction must a magnetic field be applied so that the electron moves undeflected? Ignore the gravitational force. What is the magnitude of the smallest magnetic field possible in this case?
(b) What happens if the charge is a proton that passes through the same combination of fields ?
View SolutionIf an electron enters a magnetic field with its velocity pointing in the same direction as the magnetic field, then
View Solution
