Three point masses $m_{1}, m_{2}$ and $m_{3}$ are located at the vertices of an equilateral triangle of side $α$ . What is the moment of inertia of the system about an axis along the altitude of the triangle passing through $m_{1} ?$

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the moment of inertia of the system of three point masses located at the vertices of an equilateral triangle about an axis along the altitude of the triangle passing through one of the masses, we can follow these steps:
1. Identify the Configuration:
We have three point masses $m_{1}, m_{2},$ and $m_{3}$ located at the vertices of an equilateral triangle with side length $α$ . The axis of rotation is along the altitude of the triangle passing through mass $m_{1}$ .
2. Determine the Position of the Masses:
In an equilateral triangle, the altitude divides the triangle into two right triangles. The length of the altitude $h$ can be calculated using the formula:
$h = \frac{\sqrt{3}}{2} α$
The distance from the vertex $m_{1}$ to the midpoint of the opposite side (where $m_{2}$ and $m_{3}$ are located) is $\frac{α}{2}$ .
3. Calculate the Perpendicular Distances:
- The distance $r_{1}$ of mass $m_{1}$ from the axis is $0$ (since it lies on the axis).
- The distances $r_{2}$ and $r_{3}$ of masses $m_{2}$ and $m_{3}$ from the axis are both $\frac{α}{2}$ .
4. Apply the Moment of Inertia Formula:
The moment of inertia $I$ about the axis is given by the sum of the products of each mass and the square of its distance from the axis:
$I = m_{1} r_{1}^{2} + m_{2} r_{2}^{2} + m_{3} r_{3}^{2}$
Substituting the values:
$I = m_{1} (0)^{2} + m_{2} {(\frac{α}{2})}^{2} + m_{3} {(\frac{α}{2})}^{2}$
Simplifying this gives:
$I = 0 + m_{2} (\frac{α^{2}}{4}) + m_{3} (\frac{α^{2}}{4})$
$I = \frac{α^{2}}{4} (m_{2} + m_{3})$
5. Final Result:
Therefore, the moment of inertia of the system about the specified axis is:
$I = \frac{α^{2}}{4} (m_{2} + m_{3})$

Updated on:18/9/2024

Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is

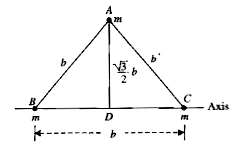A $3 m b^{2}$
B $m b^{2}$
C $(3 / 4) m b^{2}$
D $(2 / 3) m b^{2}$
Three particles of masses $1 k g, \frac{3}{2} k g, and 2 k g$ are located the vertices of an equilateral triangle of side $a$ . The $x, y$ coordinates of the centre of mass are.
Aa. $\frac{5 a}{9}, \frac{2 a}{3 \sqrt{3}}$
Bb. $\frac{2 a}{3 \sqrt{3}}, \frac{5 a}{9}$
Cc. $\frac{5 a}{9}, \frac{2 a}{\sqrt{3}}$
Dd. $\frac{2 a}{\sqrt{3}}, \frac{5 a}{9}$