Three masses of 2 kg, 3 kg and 4 kg are located at the three vertices of an equilateral triangle of side 1 m. What is the M.I. of the system about an axis along the altitude of the triangle and passing through the 3 kg mass?
The correct Answer is:10.5kgm2
To find the moment of inertia (M.I.) of the system about an axis along the altitude of the triangle and passing through the 3 kg mass, we can follow these steps:
Step 1: Understand the Configuration
We have three masses located at the vertices of an equilateral triangle with each side measuring 1 meter. The masses are:
- Mass m1=2kg at vertex A
- Mass m2=3kg at vertex B (this is where the axis passes through)
- Mass m3=4kg at vertex C
Step 2: Determine the Position of the Masses
In an equilateral triangle, the altitude divides the base into two equal halves. The distance from the vertex B (where the 3 kg mass is located) to the midpoint of the opposite side (which is the base) is 12 meter.
Step 3: Calculate the Moment of Inertia
The moment of inertia I for a system of point masses is given by the formula:
I=∑mir2i
where mi is the mass and ri is the perpendicular distance from the axis of rotation.
1. For the 3 kg mass (at vertex B):
- Distance r2=0 (since the axis passes through this mass)
- Contribution to M.I: I2=m2⋅r22=3⋅02=0
2. For the 2 kg mass (at vertex A):
- Distance r1=12 meter (perpendicular distance from the axis)
- Contribution to M.I:
I1=m1⋅r21=2⋅(12)2=2⋅14=12kg m2
3. For the 4 kg mass (at vertex C):
- Distance r3=12 meter (perpendicular distance from the axis)
- Contribution to M.I:
I3=m3⋅r23=4⋅(12)2=4⋅14=1kg m2
Step 4: Sum the Contributions
Now, we sum the contributions from all three masses:
Inet=I1+I2+I3=12+0+1=32kg m2
Final Answer
The moment of inertia of the system about the given axis is:
Inet=32kg m2
---
We have three masses located at the vertices of an equilateral triangle with each side measuring 1 meter. The masses are:
- Mass m1=2kg at vertex A
- Mass m2=3kg at vertex B (this is where the axis passes through)
- Mass m3=4kg at vertex C
In an equilateral triangle, the altitude divides the base into two equal halves. The distance from the vertex B (where the 3 kg mass is located) to the midpoint of the opposite side (which is the base) is 12 meter.
The moment of inertia I for a system of point masses is given by the formula:
I=∑mir2i
where mi is the mass and ri is the perpendicular distance from the axis of rotation.
- Distance r2=0 (since the axis passes through this mass)
- Contribution to M.I: I2=m2⋅r22=3⋅02=0
- Distance r1=12 meter (perpendicular distance from the axis)
- Contribution to M.I:
I1=m1⋅r21=2⋅(12)2=2⋅14=12kg m2
- Distance r3=12 meter (perpendicular distance from the axis)
- Contribution to M.I:
I3=m3⋅r23=4⋅(12)2=4⋅14=1kg m2
Now, we sum the contributions from all three masses:
Inet=I1+I2+I3=12+0+1=32kg m2
The moment of inertia of the system about the given axis is:
Inet=32kg m2
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)14videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM CENTRE OF MASS)8videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
Similar Questions
Three point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View Solution
Knowledge Check
- Question 1 - Select One
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
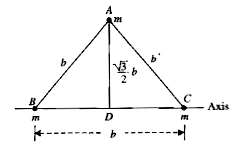 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2 - Question 2 - Select One
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
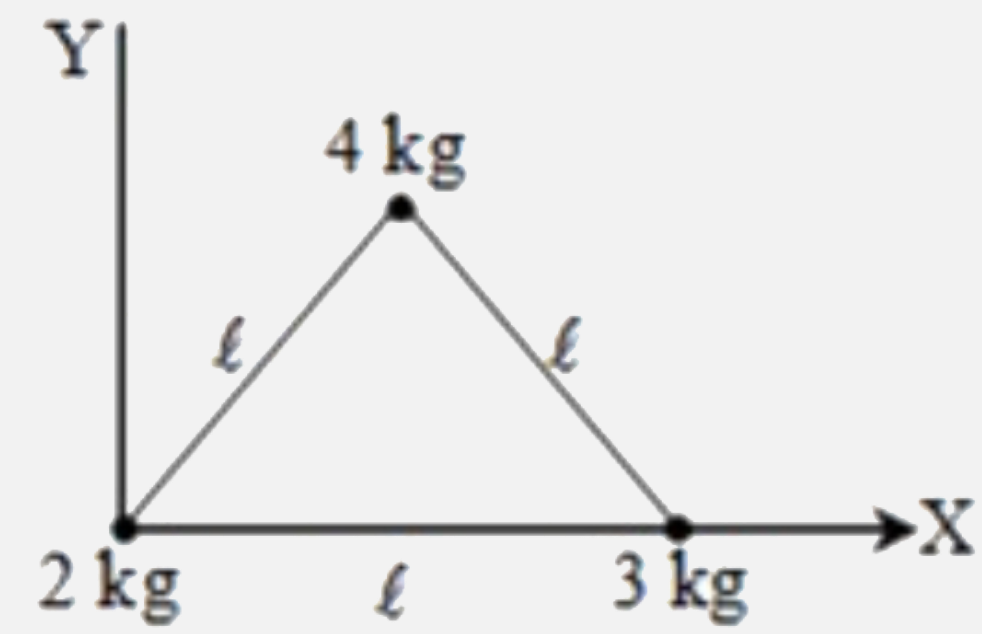 View Solution
View SolutionThree masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
View SolutionThree balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionThree masses of 1 kg each are kept at the vertices of an equilateral triangle of side 3 m. What is the force acting on a point mass of 5 kg placed at its centroid ?
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View Solution

