A hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
To solve the problem step by step, we will analyze the situation before and after the collision, applying the principles of conservation of angular momentum and the conditions for rolling without slipping.
Step 1: Understand the Initial Conditions
A hollow sphere of mass M is at rest on a rough horizontal plane. A particle of mass m is moving with speed v and collides with the sphere at a height h above the center of the sphere.
Step 2: Conservation of Angular Momentum
Since there are no external torques acting on the system, we can use the conservation of angular momentum about the center of the hollow sphere (point O).
- Initial Angular Momentum: The only object contributing to angular momentum before the collision is the particle of mass m:
Linitial=m⋅v⋅h
- Final Angular Momentum: After the collision, both the mass m and the hollow sphere rotate together with an angular velocity ω. The moment of inertia I of the system (hollow sphere + mass) is:
I=23MR2+mR2
Therefore, the final angular momentum is:
Lfinal=I⋅ω=(23MR2+mR2)⋅ω
Step 3: Set Up the Equation
By conservation of angular momentum:
mvh=(23MR2+mR2)⋅ω
Step 4: Relate Angular Velocity to Linear Velocity
For rolling without slipping, the relationship between the linear velocity of the center of mass vcm and the angular velocity ω is given by:
ω=vcmR
Step 5: Find Linear Momentum Conservation
The initial linear momentum is:
Pinitial=mv
After the collision, the total mass moving with velocity vcm is m+M:
Pfinal=(m+M)vcm
By conservation of linear momentum:
mv=(m+M)vcm
From this, we can express vcm:
vcm=mvm+M
Step 6: Substitute vcm into Angular Momentum Equation
Substituting vcm into the angular momentum equation gives:
mvh=(23MR2+mR2)⋅vcmR
This simplifies to:
mvh=(23MR2+mR2)⋅mv(m+M)R
Step 7: Cancel mv and Solve for h
Cancelling mv from both sides:
h=R(23M+m)m+M
Since m≪M, we can neglect m in comparison to M:
h≈R⋅23MM=23R
Final Answer
Thus, the height h at which the particle collides with the sphere is:
h=23R
A hollow sphere of mass M is at rest on a rough horizontal plane. A particle of mass m is moving with speed v and collides with the sphere at a height h above the center of the sphere.
Since there are no external torques acting on the system, we can use the conservation of angular momentum about the center of the hollow sphere (point O).
Linitial=m⋅v⋅h
I=23MR2+mR2
Therefore, the final angular momentum is:
Lfinal=I⋅ω=(23MR2+mR2)⋅ω
By conservation of angular momentum:
mvh=(23MR2+mR2)⋅ω
For rolling without slipping, the relationship between the linear velocity of the center of mass vcm and the angular velocity ω is given by:
ω=vcmR
The initial linear momentum is:
Pinitial=mv
After the collision, the total mass moving with velocity vcm is m+M:
Pfinal=(m+M)vcm
By conservation of linear momentum:
mv=(m+M)vcm
From this, we can express vcm:
vcm=mvm+M
Substituting vcm into the angular momentum equation gives:
mvh=(23MR2+mR2)⋅vcmR
This simplifies to:
mvh=(23MR2+mR2)⋅mv(m+M)R
Cancelling mv from both sides:
h=R(23M+m)m+M
Since m≪M, we can neglect m in comparison to M:
h≈R⋅23MM=23R
Thus, the height h at which the particle collides with the sphere is:
h=23R
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
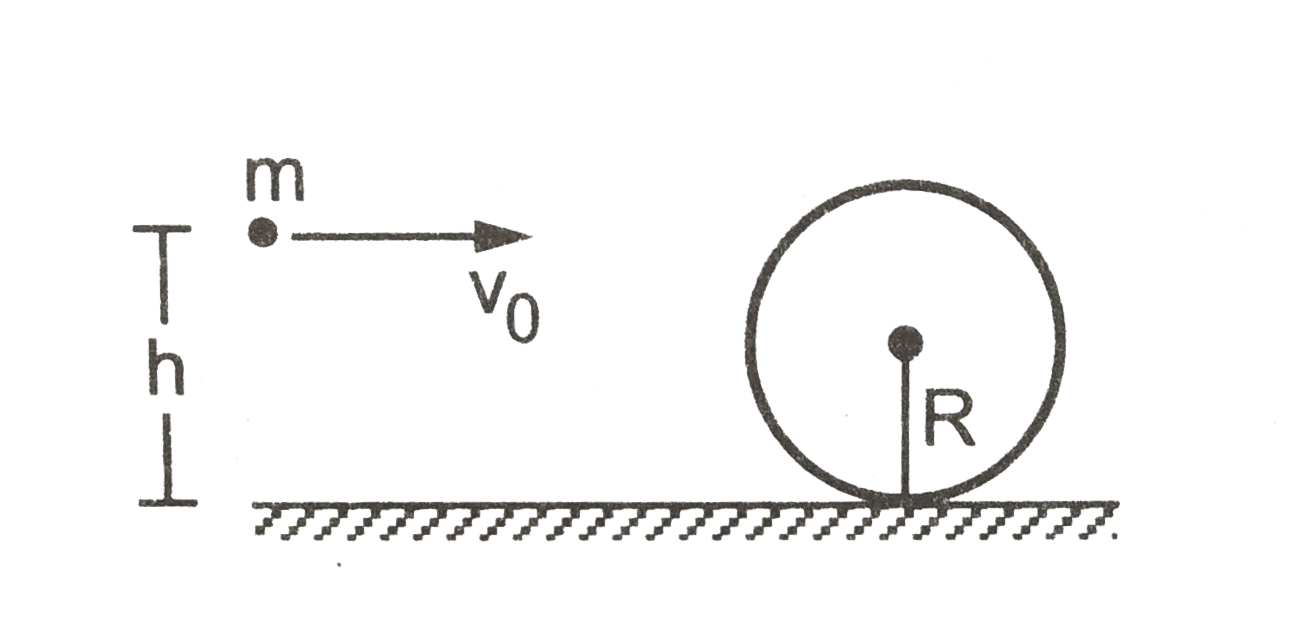
The sphere shown in figure lies on a rough plane when a particle of mass m travelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combined system just after the collision b. the angular speed of the system about the centre of the sphere just the collision c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View Solution
A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collision
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then

View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA wedge of mass M=4m lies on a frictionless plane. A particle of mass m approaches the wedge with speed v. there is no friction between the particle and the plane or between the particle and the wedge. The maximum height climbed by the particle on the wedge is given by
View SolutionA solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View Solution