A sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
3u24g
5u22g
7u210g
11u29g
The correct Answer is:C
To solve the problem of finding the maximum height attained by a sphere of mass m and radius r that rolls without slipping with an initial speed u, we can follow these steps:
Step 1: Understand the Energy Conservation Principle
When the sphere rolls up vertically, its initial kinetic energy will be converted into potential energy at the maximum height. The total mechanical energy is conserved.
Step 2: Write the Expression for Kinetic Energy
The total kinetic energy (KE) of the sphere consists of translational kinetic energy and rotational kinetic energy:
KE=KEtranslational+KErotational=12mu2+12Iω2
Step 3: Determine the Moment of Inertia
For a solid sphere, the moment of inertia I is given by:
I=25mr2
Step 4: Relate Angular Velocity to Linear Velocity
Since the sphere rolls without slipping, we have the relationship:
u=ωr⟹ω=ur
Step 5: Substitute the Values into the Kinetic Energy Equation
Substituting the moment of inertia and angular velocity into the kinetic energy equation:
KE = \frac{1}{2} m u^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right} \left(\frac{u}{r}\right)^2
This simplifies to:
KE=12mu2+12(25mr2)(u2r2)
KE=12mu2+15mu2=(510+210)mu2=710mu2
Step 6: Set the Kinetic Energy Equal to Potential Energy
At the maximum height h, all kinetic energy is converted into potential energy:
KE=PE⟹710mu2=mgh
Step 7: Solve for Maximum Height h
Cancelling m from both sides (assuming m≠0):
710u2=gh
Rearranging gives:
h=710u2g
Conclusion
The maximum height h that the sphere would attain is:
h=7u210g
When the sphere rolls up vertically, its initial kinetic energy will be converted into potential energy at the maximum height. The total mechanical energy is conserved.
The total kinetic energy (KE) of the sphere consists of translational kinetic energy and rotational kinetic energy:
KE=KEtranslational+KErotational=12mu2+12Iω2
For a solid sphere, the moment of inertia I is given by:
I=25mr2
Since the sphere rolls without slipping, we have the relationship:
u=ωr⟹ω=ur
Substituting the moment of inertia and angular velocity into the kinetic energy equation:
KE = \frac{1}{2} m u^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right} \left(\frac{u}{r}\right)^2
This simplifies to:
KE=12mu2+12(25mr2)(u2r2)
KE=12mu2+15mu2=(510+210)mu2=710mu2
At the maximum height h, all kinetic energy is converted into potential energy:
KE=PE⟹710mu2=mgh
Cancelling m from both sides (assuming m≠0):
710u2=gh
Rearranging gives:
h=710u2g
The maximum height h that the sphere would attain is:
h=7u210g
Similar Questions
A mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionAn object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
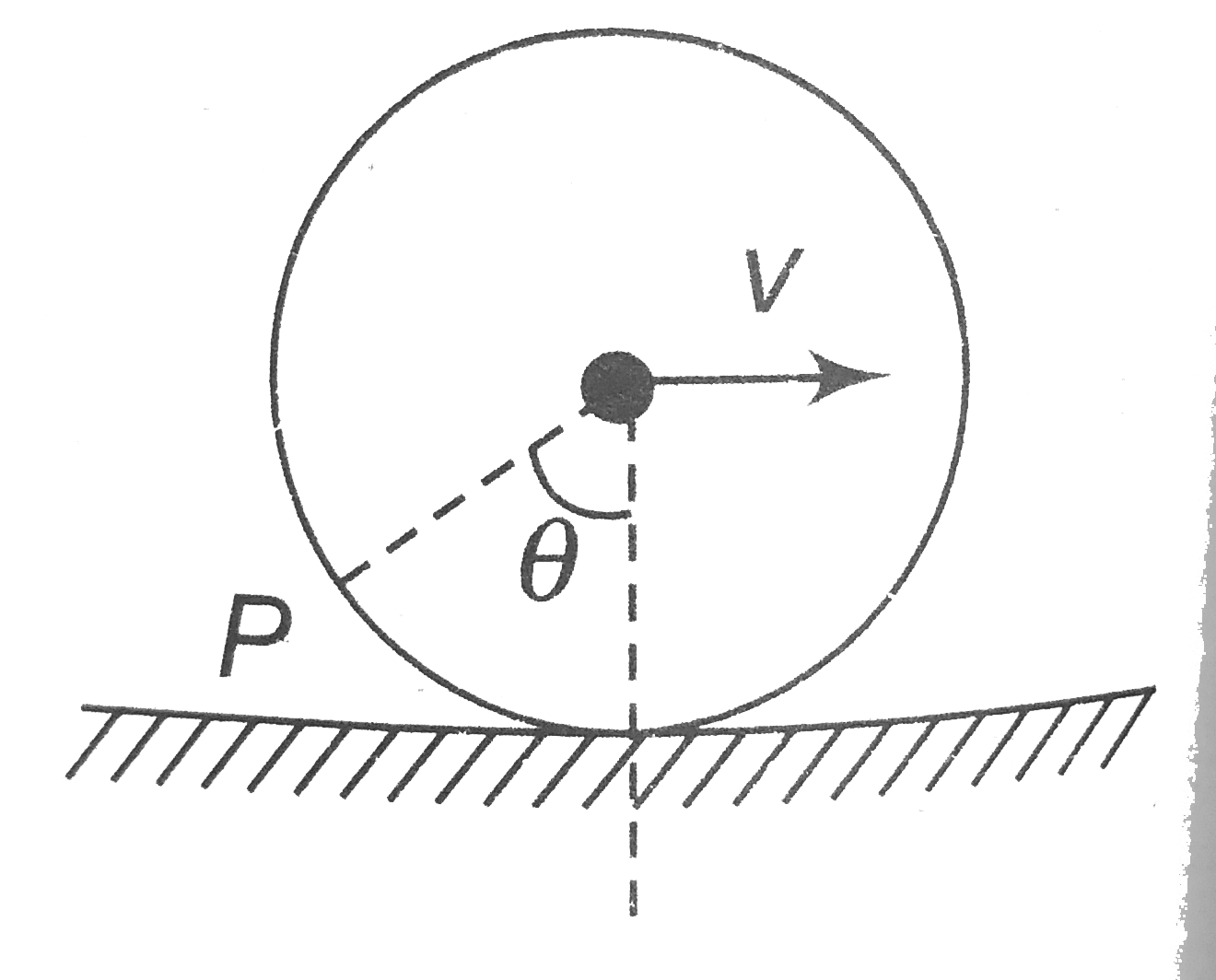
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
View Solution
