Two identical spherical masses are kept at some distance. Potential energy when a mass m is taken from the surface of one sphere to the other
increases continuously
decreases continuously
first increases then decreases
first decreases then increases
The correct Answer is:C
To solve the problem of finding the potential energy when a mass m is taken from the surface of one identical spherical mass to the surface of another identical spherical mass, we can follow these steps:
Step 1: Understand the System
We have two identical spherical masses, each of mass M, separated by a distance R. We want to calculate the gravitational potential energy when a mass m is moved from the surface of one sphere to the surface of the other.
Step 2: Calculate the Initial Potential Energy
The gravitational potential energy U between two masses M and m separated by a distance d is given by the formula:
U=−GMmd
Initially, when the mass m is on the surface of the first sphere, the distance from the center of the first sphere to the center of the second sphere is R. Therefore, the initial potential energy Ui when m is on the surface of the first sphere is:
Ui=−GMmR
Step 3: Calculate the Final Potential Energy
When the mass m is moved to the surface of the second sphere, the distance from the center of the second sphere to the mass m is still R. Thus, the final potential energy Uf when the mass m is on the surface of the second sphere is:
Uf=−GMmR
Step 4: Calculate the Change in Potential Energy
The change in potential energy ΔU when moving the mass m from the first sphere to the second sphere is given by:
ΔU=Uf−Ui
Since both Ui and Uf are equal:
ΔU=−GMmR−(−GMmR)=0
Conclusion
The gravitational potential energy does not change when moving the mass m from the surface of one identical sphere to the surface of another identical sphere. Thus, the potential energy remains constant at:
ΔU=0
We have two identical spherical masses, each of mass M, separated by a distance R. We want to calculate the gravitational potential energy when a mass m is moved from the surface of one sphere to the surface of the other.
The gravitational potential energy U between two masses M and m separated by a distance d is given by the formula:
U=−GMmd
Initially, when the mass m is on the surface of the first sphere, the distance from the center of the first sphere to the center of the second sphere is R. Therefore, the initial potential energy Ui when m is on the surface of the first sphere is:
Ui=−GMmR
When the mass m is moved to the surface of the second sphere, the distance from the center of the second sphere to the mass m is still R. Thus, the final potential energy Uf when the mass m is on the surface of the second sphere is:
Uf=−GMmR
The change in potential energy ΔU when moving the mass m from the first sphere to the second sphere is given by:
ΔU=Uf−Ui
Since both Ui and Uf are equal:
ΔU=−GMmR−(−GMmR)=0
The gravitational potential energy does not change when moving the mass m from the surface of one identical sphere to the surface of another identical sphere. Thus, the potential energy remains constant at:
ΔU=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2A larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for m=k(M288). The value of k is
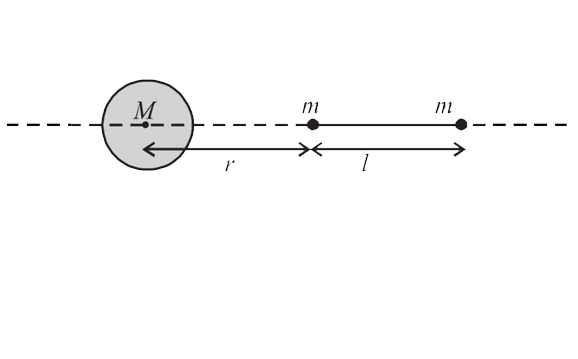 A5B6C7D8
A5B6C7D8
Two celestial bodies are separated by some distance. If the mass of any one of the bodies is doubled while the mass of other is halved then how far should they be taken so that the gravitational force between them becomes one-fourth ?
View SolutionTwo celestial bodies are separated by some distance. If the mass of any one of the bodies is doubled while the mass of other is halved then how far should they be taken so that the gravitational force between them becomes one-fourth ?
View SolutionFigure shows 4 identical masses of mass m, arranged on a cube as shown.
The potential energy of the system is
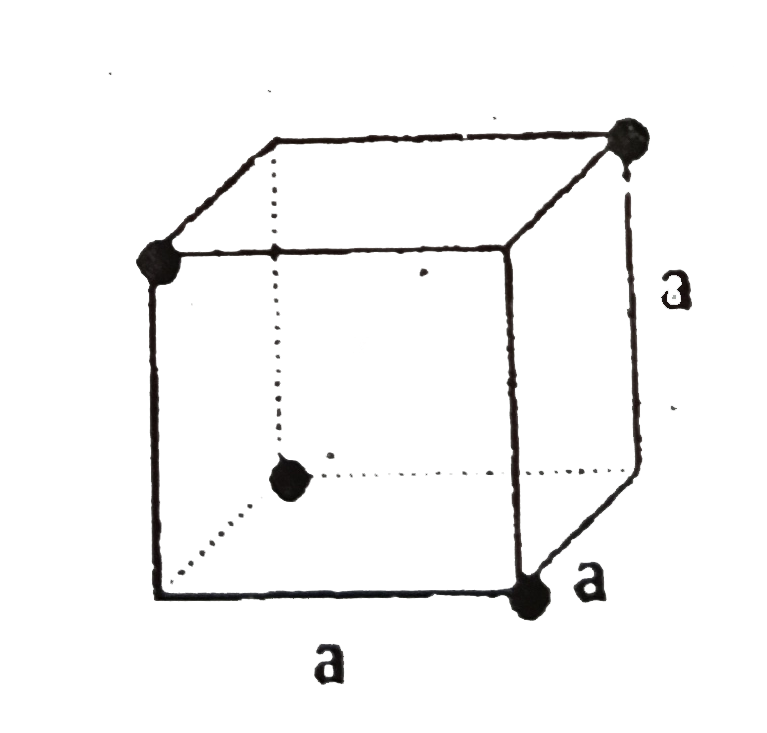
View SolutionA mass is taken from surface to a height h. The change in potential energy in this process is equal to the change in potential energy if it is now taken from that point to infinity. What is the value of h?
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View Solution
