If radius of a solid sohere is decreases to half, keeping density of sphere unchanged, the slope of E-r graph inside the sphere will
remain unchanged
become two times
become four times
remain 18 th
The correct Answer is:A
To solve the problem, we need to analyze how the gravitational field inside a solid sphere changes when the radius is decreased to half while keeping the density constant. Let's break this down step by step.
1. Understanding the Gravitational Field Inside a Solid Sphere:
The gravitational field E inside a solid sphere at a distance r from the center is given by the formula:
E=GM(r)r2
where M(r) is the mass enclosed within radius r.
2. Finding the Mass Enclosed:
The mass M of the sphere can be expressed in terms of density ρ and volume V:
M=ρV
For a sphere, the volume V is given by:
V=43πR3
Therefore, the mass of the sphere is:
M=ρ(43πR3)
3. Substituting Mass in the Gravitational Field Equation:
Substituting the expression for mass into the gravitational field equation gives:
E=G(ρ43πR3)r2
4. Finding the Slope of the E-r Graph:
The slope of the E−r graph can be derived from the gravitational field equation. The slope S can be expressed as:
S=Gρ43πR3r2
Since we are interested in the slope at a specific radius r, we can simplify this to:
S=Gρ4π3
Here, we note that the slope depends on G and ρ but not on R or r.
5. Effect of Decreasing Radius:
When the radius R is decreased to half, the density ρ remains unchanged. Thus, the expression for the slope does not change because it does not depend on R directly.
6. Conclusion:
Since the slope S is independent of the radius R and only depends on the constants G and ρ, the slope of the E−r graph remains unchanged when the radius is halved.
Final Answer:
The slope of the E−r graph inside the sphere will remain unchanged.
The gravitational field E inside a solid sphere at a distance r from the center is given by the formula:
E=GM(r)r2
where M(r) is the mass enclosed within radius r.
The mass M of the sphere can be expressed in terms of density ρ and volume V:
M=ρV
For a sphere, the volume V is given by:
V=43πR3
Therefore, the mass of the sphere is:
M=ρ(43πR3)
Substituting the expression for mass into the gravitational field equation gives:
E=G(ρ43πR3)r2
The slope of the E−r graph can be derived from the gravitational field equation. The slope S can be expressed as:
S=Gρ43πR3r2
Since we are interested in the slope at a specific radius r, we can simplify this to:
S=Gρ4π3
Here, we note that the slope depends on G and ρ but not on R or r.
When the radius R is decreased to half, the density ρ remains unchanged. Thus, the expression for the slope does not change because it does not depend on R directly.
Since the slope S is independent of the radius R and only depends on the constants G and ρ, the slope of the E−r graph remains unchanged when the radius is halved.
The slope of the E−r graph inside the sphere will remain unchanged.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a sphere of radius 3 is inscribed in a cube such that it is tangent to all six faces of the cube, the volume contained outside the sphere and inside the cube is
A97B103C109D115Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionThree spheres of radius 'r' are kept inside a cuylinder such that two of the speres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder .Find the volume of the cylinder .
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
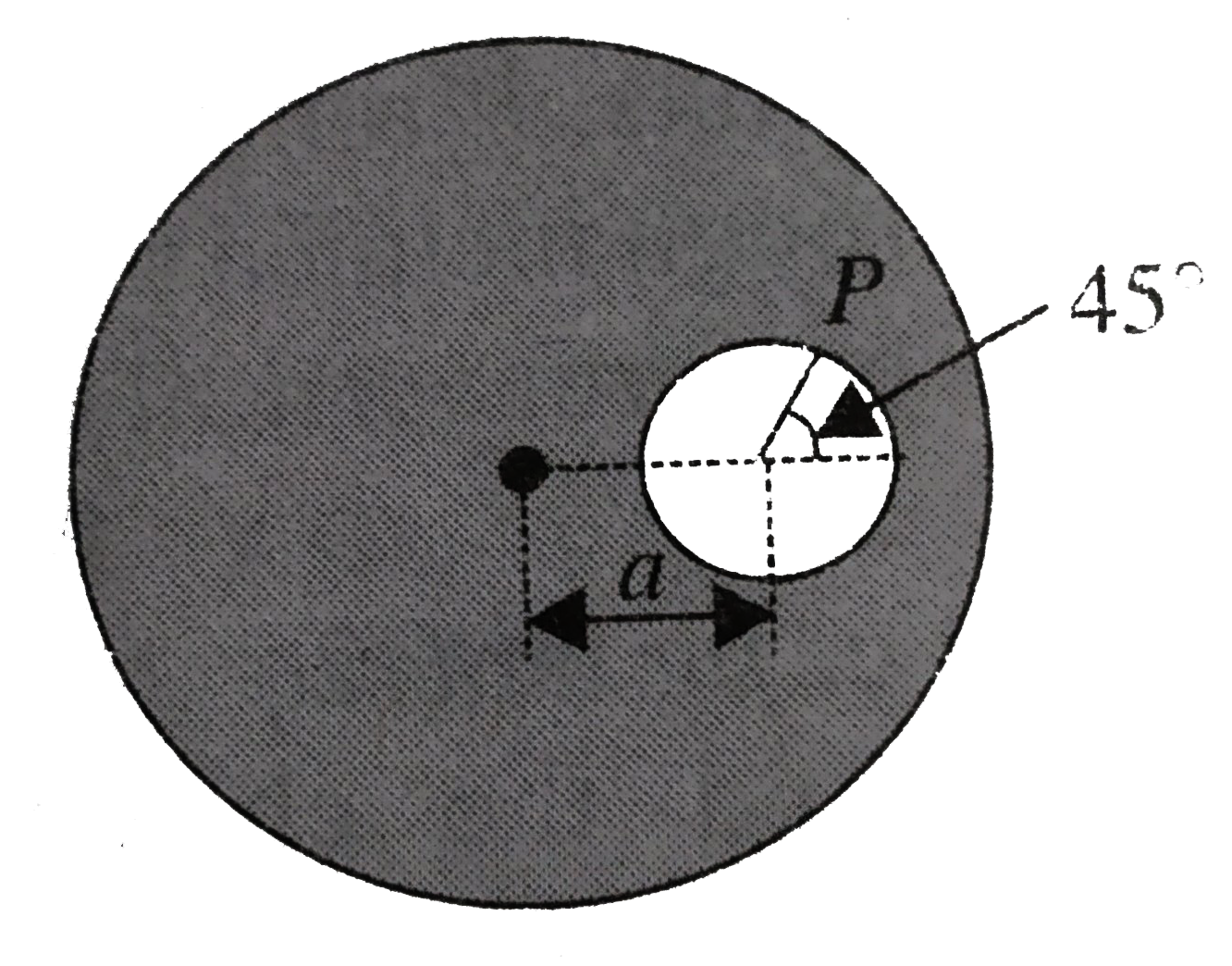
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View Solution
