A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
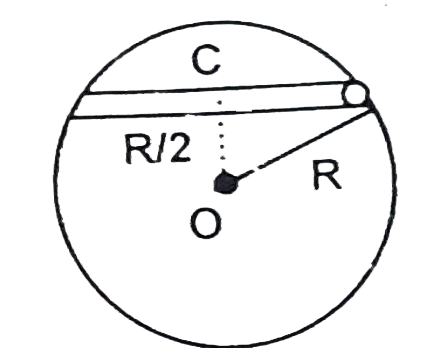
√3GM2R
√3GM4R
√3GM8R
d√3GM16R
The correct Answer is:B
Using conservation of energy
12mv2=−GMmR−(−11GMm8R)
12mv2=3GMn8R
∴V=√3GM4R
Similar Questions
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
View SolutionA tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
View SolutionA body starts from rest from a point distant r0 from the centre of the earth. It reaches the surface of the earth whose radius is R. The velocity acquired by the body is
View SolutionA body starts from rest from a point distant r0 from the centre of the earth. It reaches the surface of the earth whose radius is R. The velocity acquired by the body is
View SolutionA tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionA ball of mass m and radius r rolls inside a hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
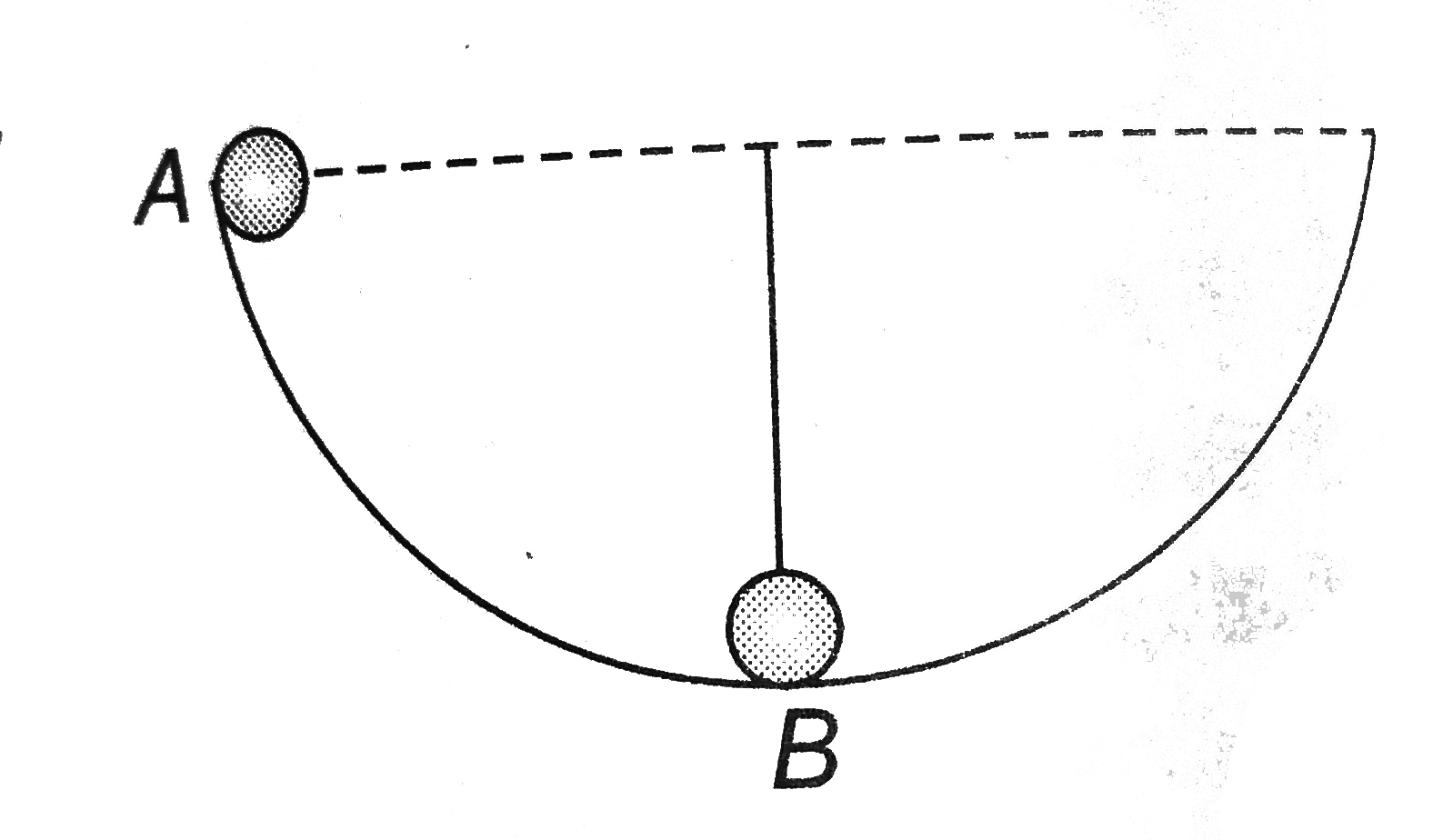 .View Solution
.View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionA satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of
View SolutionA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View SolutionThe distances from the centre of the earth, where the weight of a body is zero and one-fourth that of the weight of the body on the surface of the earth are (assume R is the radius of the earth)
View Solution

