A tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after
84.6 min
42.3 min
1 day
will not reach the other end
The correct Answer is:B
(b)Ball will execute SHM inside the tunnel with time period
T=2π√R/g=84.63 min
Hence, time do reach the ball from one end to the other end of the tunnel t=84.632=43.3 min.
Similar Questions
A tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
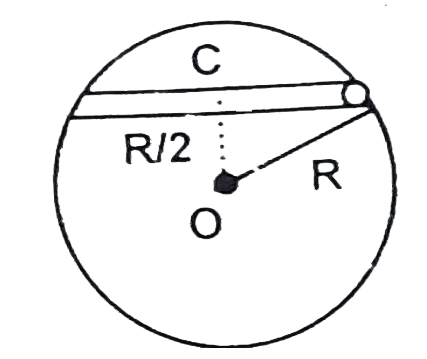 View Solution
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.
 View Solution
View SolutionA tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionA tunnel is dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle isView SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal toView SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
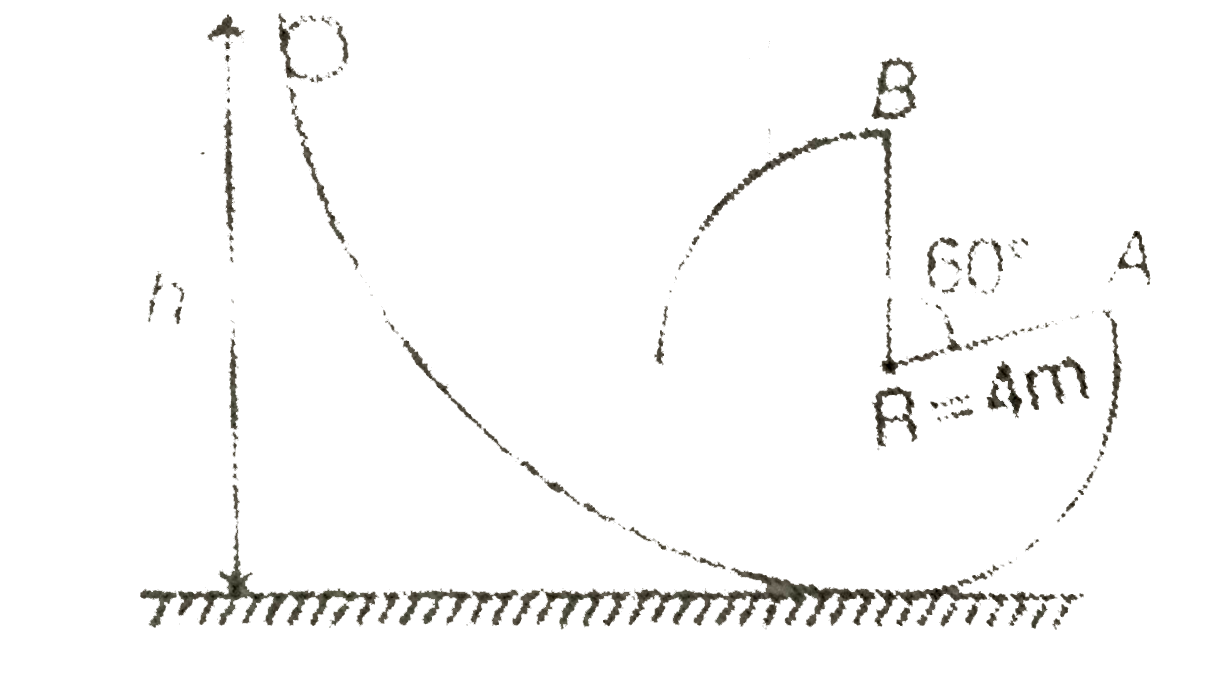 View Solution
View Solution

