In an LR circuit, current at t=0 is 20A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
In(109)
2
2In(109)
2In(109)
The correct Answer is:C
To solve the problem, we will use the decay equation for current in an LR circuit, which is given by:
I(t)=I0⋅e−t/τ
where:
- I(t) is the current at time t,
- I0 is the initial current,
- τ is the time constant,
- e is the base of the natural logarithm.
1. Identify the given values:
- Initial current, I0=20A
- Current after 2 seconds, I(2)=18A
- Time, t=2s
2. Write the decay equation for the current at t=2s:
I(2)=I0⋅e−2/τ
Substituting the known values:
18=20⋅e−2/τ
3. Rearrange the equation to isolate the exponential term:
e−2/τ=1820=910
4. Take the natural logarithm of both sides:
−2τ=ln(910)
5. Solve for τ:
2τ=−ln(910)
τ=2−ln(910)
6. Using properties of logarithms:
−ln(910)=ln(109)
Thus, we can rewrite τ:
τ=2ln(109)
Final Answer:
The time constant τ of the circuit is:
τ=2ln(109) seconds
- I(t) is the current at time t,
- I0 is the initial current,
- τ is the time constant,
- e is the base of the natural logarithm.
- Initial current, I0=20A
- Current after 2 seconds, I(2)=18A
- Time, t=2s
I(2)=I0⋅e−2/τ
Substituting the known values:
18=20⋅e−2/τ
e−2/τ=1820=910
−2τ=ln(910)
2τ=−ln(910)
τ=2−ln(910)
−ln(910)=ln(109)
Thus, we can rewrite τ:
τ=2ln(109)
The time constant τ of the circuit is:
τ=2ln(109) seconds
Topper's Solved these Questions
Similar Questions
Time constant of LR circuit will be
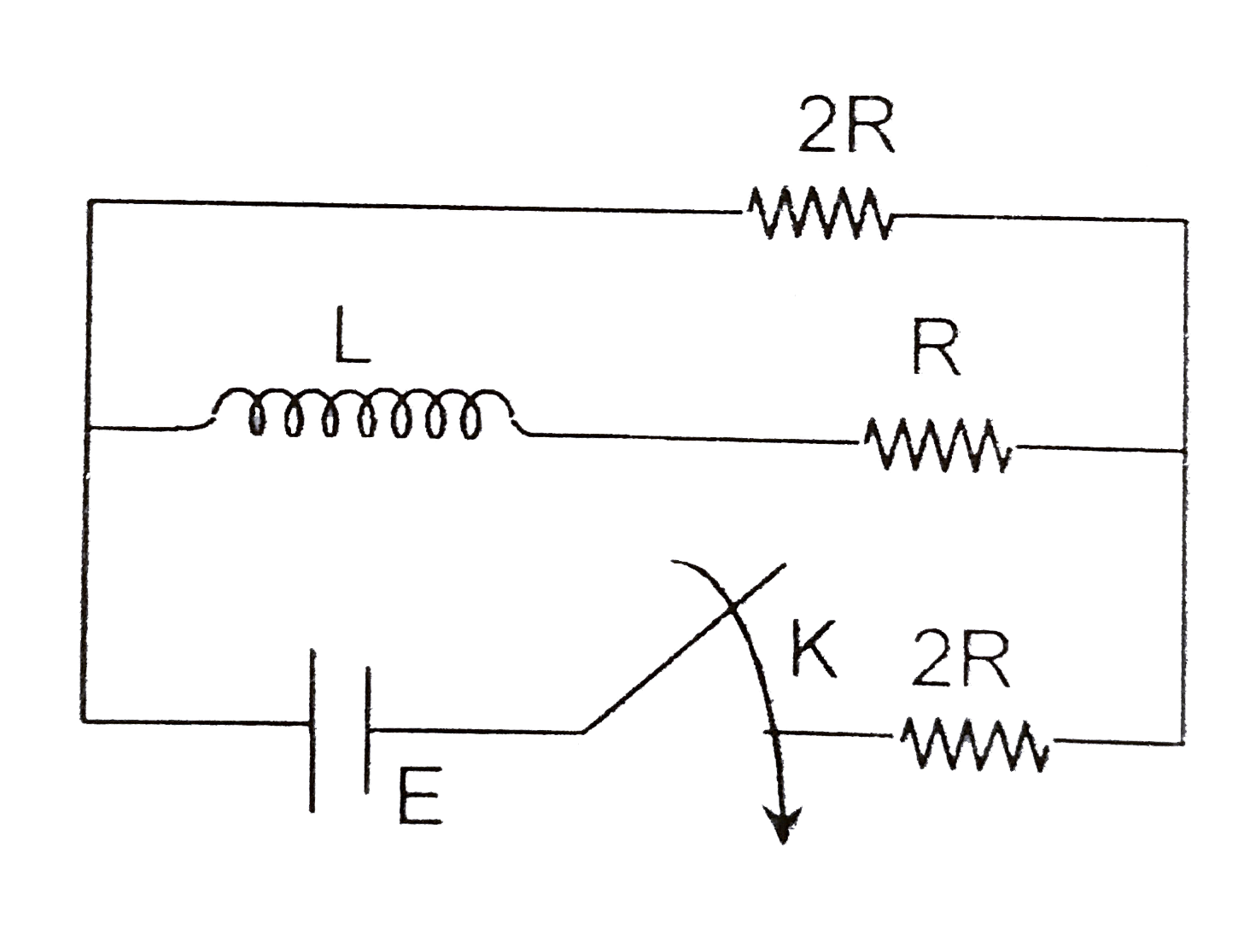
View SolutionIn the transient circuit shown, the time constant of the circuit is :
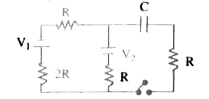
View SolutionA coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
View SolutionConsider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
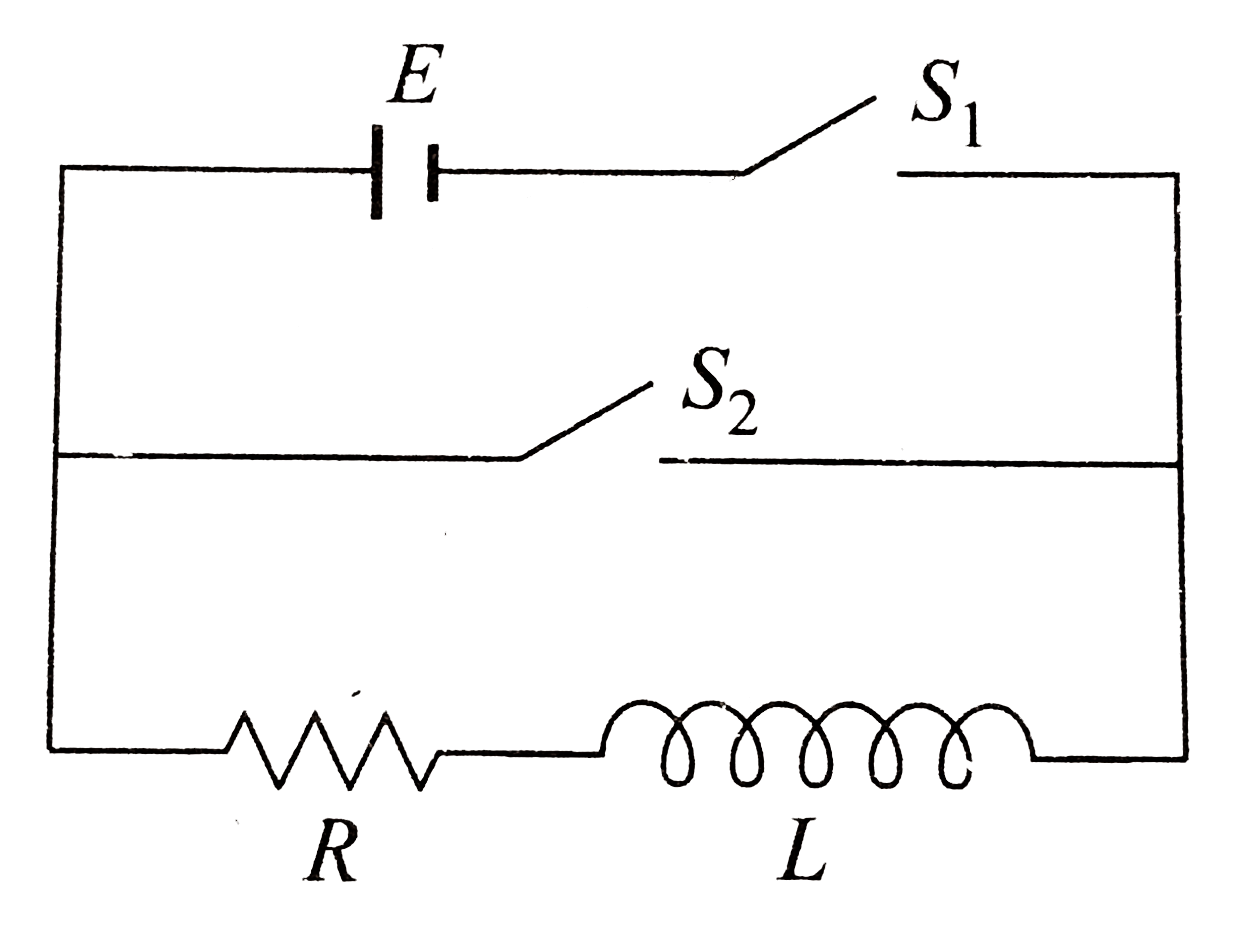
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit is
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 1.0A in 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
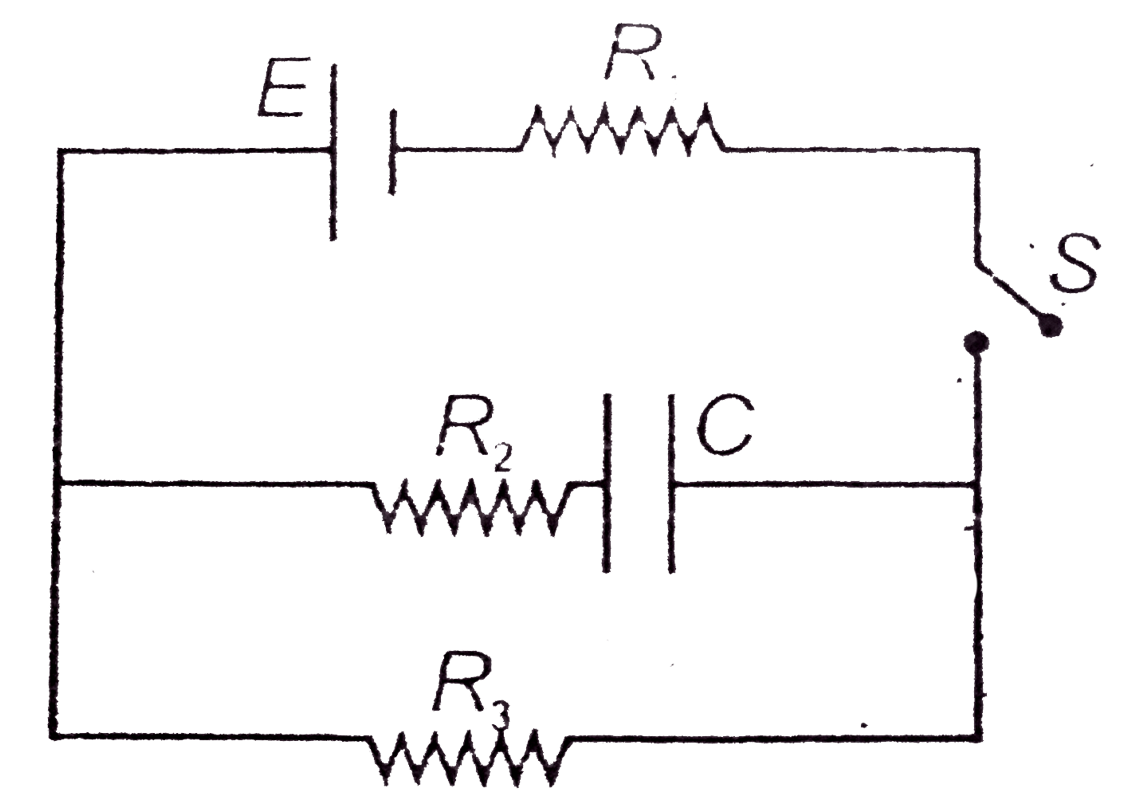
View SolutionFind time constant of the circuit when (a) S is closed . (b) S is open.
View SolutionA coil of inductance 2H and resistance 10Ω are in a series circuit with an open key and a cell of constant 100V with negligible resistance. At time i=0, the key is closed. Find
(a) the time constant of the circuit.
(b) the maximum steady current in the circuit.
(c) the current in the circuit at f=1s.
View Solution
In given LR circuit the switch S is closed at time t=0 then
View Solution
