A non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
The correct Answer is:C
To solve the problem, we need to analyze the situation involving a non-conducting ring placed on a rough horizontal surface in a time-varying magnetic field. We will derive the expression for the coefficient of friction (μ) that allows the ring to start rotating after 2 seconds.
1. Identify the Magnetic Field and its Rate of Change:
The magnetic field is given by B=4t2. To find the induced electromotive force (EMF), we first need to calculate the rate of change of the magnetic field:
dBdt=ddt(4t2)=8t
2. Calculate the Induced EMF:
The induced EMF (ε) in the ring can be calculated using Faraday's law of electromagnetic induction:
ϵ=−dΦdt
where Φ is the magnetic flux. The area A of the ring is πR2, thus:
Φ=B⋅A=B⋅πR2=4t2⋅πR2
Therefore, the induced EMF is:
ϵ=−ddt(4t2⋅πR2)=−8t⋅πR2
3. Determine the Induced Electric Field:
The induced electric field E can be related to the induced EMF by the formula:
ϵ=E⋅(2πR)
Thus, we can express the electric field as:
E=ϵ2πR=−8t⋅πR22πR=−4tR
4. Calculate the Torque due to Electric Force:
The electric force F acting on the charge q distributed uniformly on the ring due to the electric field is:
F=qE=q(−4tR)=−4qtR
The torque τ caused by this force about the center of the ring is:
τ=F⋅R=−4qtR2
5. Calculate the Torque due to Friction:
The torque due to friction τf that opposes the motion is given by:
τf=μmgR
6. Set the Torques Equal at t = 2 seconds:
The ring starts rotating at t=2 seconds, so we set the magnitudes of the torques equal:
4q(2)R2=μmgR
7. Solve for the Coefficient of Friction (μ):
Rearranging the equation gives:
μ=4q(2)R2mgR=8qRmg
Final Expression for Coefficient of Friction:
μ=8qRmg
The magnetic field is given by B=4t2. To find the induced electromotive force (EMF), we first need to calculate the rate of change of the magnetic field:
dBdt=ddt(4t2)=8t
The induced EMF (ε) in the ring can be calculated using Faraday's law of electromagnetic induction:
ϵ=−dΦdt
where Φ is the magnetic flux. The area A of the ring is πR2, thus:
Φ=B⋅A=B⋅πR2=4t2⋅πR2
Therefore, the induced EMF is:
ϵ=−ddt(4t2⋅πR2)=−8t⋅πR2
The induced electric field E can be related to the induced EMF by the formula:
ϵ=E⋅(2πR)
Thus, we can express the electric field as:
E=ϵ2πR=−8t⋅πR22πR=−4tR
The electric force F acting on the charge q distributed uniformly on the ring due to the electric field is:
F=qE=q(−4tR)=−4qtR
The torque τ caused by this force about the center of the ring is:
τ=F⋅R=−4qtR2
The torque due to friction τf that opposes the motion is given by:
τf=μmgR
The ring starts rotating at t=2 seconds, so we set the magnitudes of the torques equal:
4q(2)R2=μmgR
Rearranging the equation gives:
μ=4q(2)R2mgR=8qRmg
μ=8qRmg
Similar Questions
A conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
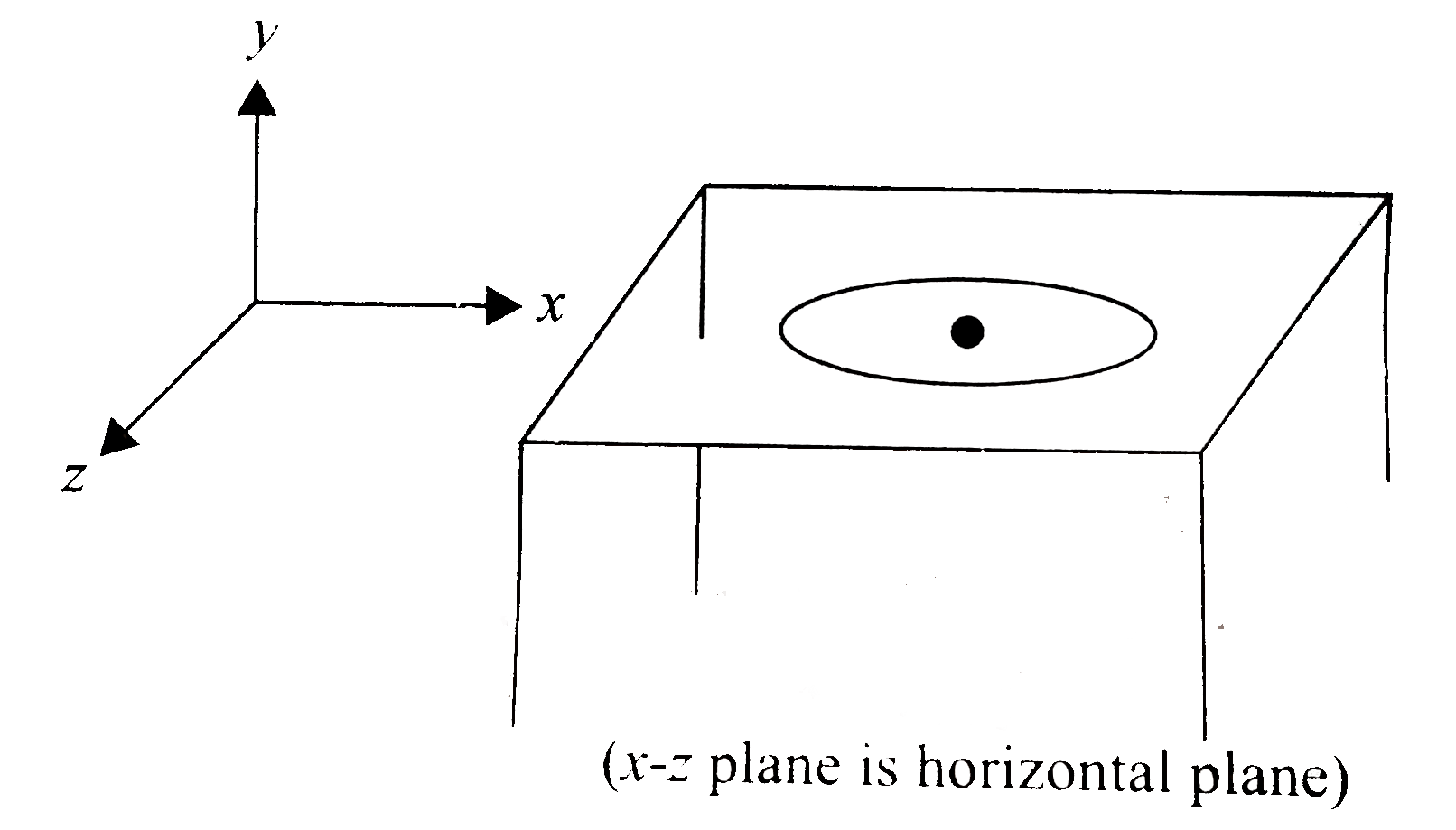
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)

View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
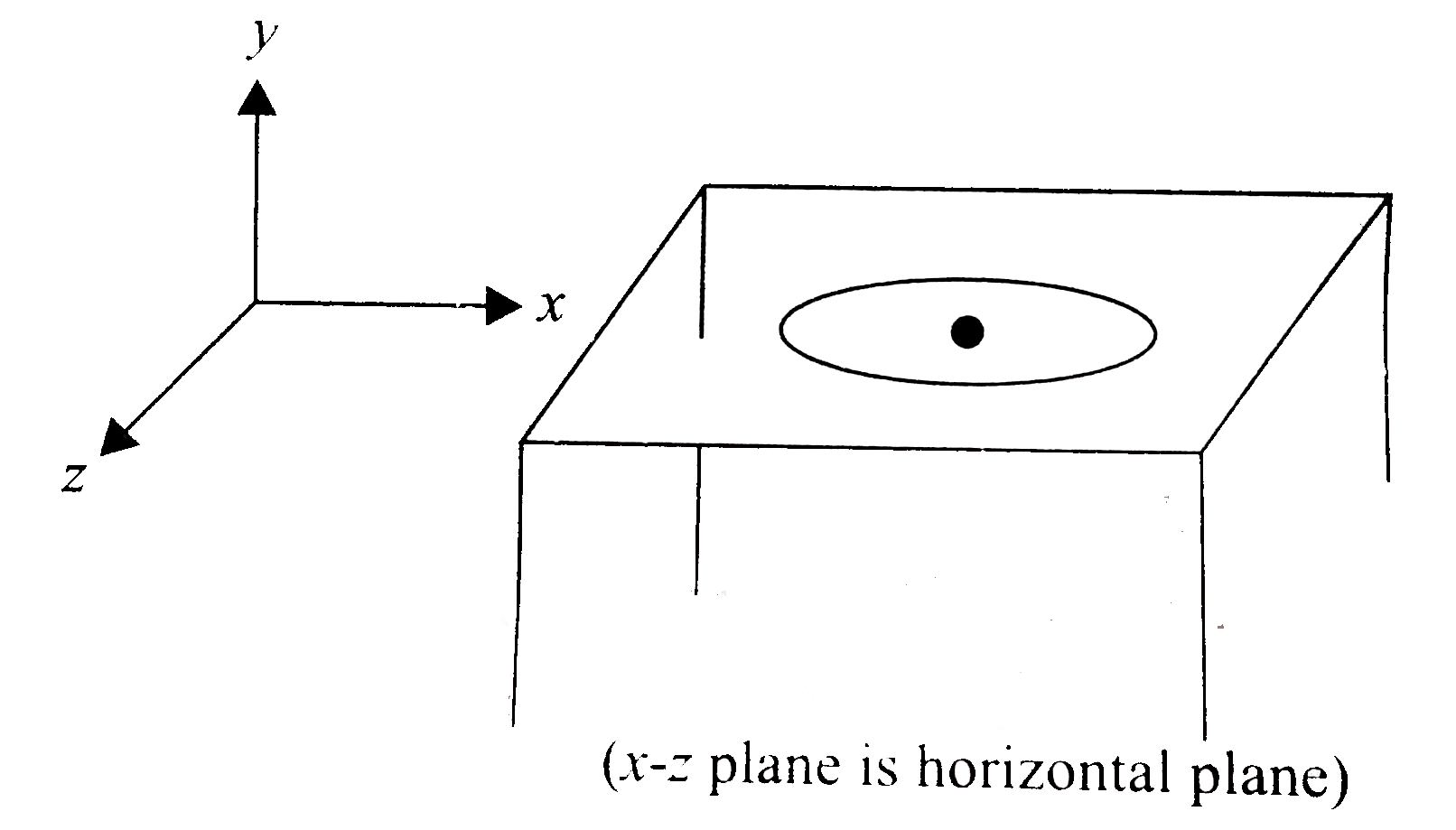
Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling is
View Solution
Charge 'q' is uniformly distributed along the length of a non-coducting circular ring of mass m and radius 'a'. The ring is placed concentrically magnetic field B=kt (where k is constant) is existing perpendicular to the plane of circular region of radius 'R' as shown. The minimum coefficient of friction between the ring and the surface required to keep the ring stationary is
View Solution
