A capacitor in an LC oscillation has a maximum potential difference of 1.5 and a maximum energy 360μJ. At a certain instant the energy in the capacitor is 40μJ, the potential difference across the capacitor is V volt?
0 volt
5 volt
15 volt
20volt
The correct Answer is:B, C
To solve the problem step by step, we will use the formulas related to the energy stored in a capacitor and the relationship between energy, capacitance, and voltage.
Step 1: Understand the given values
We are given:
- Maximum potential difference across the capacitor, Vmax=1.5V
- Maximum energy stored in the capacitor, EC=360μJ=360×10−6J
- Energy at a certain instant, EC′=40μJ=40×10−6J
Step 2: Use the energy formula for a capacitor
The energy stored in a capacitor is given by the formula:
EC=12CV2
Where:
- EC is the energy stored in the capacitor,
- C is the capacitance,
- V is the potential difference across the capacitor.
Step 3: Find the capacitance C
Using the maximum energy and maximum potential difference:
360×10−6=12C(1.5)2
Calculating (1.5)2:
(1.5)2=2.25
Now substituting this back into the equation:
360×10−6=12C(2.25)
Rearranging to find C:
C=2×360×10−62.25
Calculating the right-hand side:
C=720×10−62.25=320×10−6F=3.2μF
Step 4: Use the energy formula for the instant energy
Now, we need to find the potential difference V′ when the energy is 40μJ:
EC′=12C(V′)2
Substituting the known values:
40×10−6=12(3.2×10−6)(V′)2
Rearranging to solve for V′:
40×10−6=1.6×10−6(V′)2
Dividing both sides by 1.6×10−6:
40×10−61.6×10−6=(V′)2
Calculating the left-hand side:
401.6=25
Thus,
(V′)2=25
Taking the square root:
V′=√25=5V
Final Answer
The potential difference across the capacitor at that instant is V′=5V.
---
We are given:
- Maximum potential difference across the capacitor, Vmax=1.5V
- Maximum energy stored in the capacitor, EC=360μJ=360×10−6J
- Energy at a certain instant, EC′=40μJ=40×10−6J
The energy stored in a capacitor is given by the formula:
EC=12CV2
Where:
- EC is the energy stored in the capacitor,
- C is the capacitance,
- V is the potential difference across the capacitor.
Using the maximum energy and maximum potential difference:
360×10−6=12C(1.5)2
Calculating (1.5)2:
(1.5)2=2.25
Now substituting this back into the equation:
360×10−6=12C(2.25)
Rearranging to find C:
C=2×360×10−62.25
Calculating the right-hand side:
C=720×10−62.25=320×10−6F=3.2μF
Now, we need to find the potential difference V′ when the energy is 40μJ:
EC′=12C(V′)2
Substituting the known values:
40×10−6=12(3.2×10−6)(V′)2
Rearranging to solve for V′:
40×10−6=1.6×10−6(V′)2
Dividing both sides by 1.6×10−6:
40×10−61.6×10−6=(V′)2
Calculating the left-hand side:
401.6=25
Thus,
(V′)2=25
Taking the square root:
V′=√25=5V
The potential difference across the capacitor at that instant is V′=5V.
Similar Questions
In the adjoning figure, the potential difference across the 4.5μF capacitor is

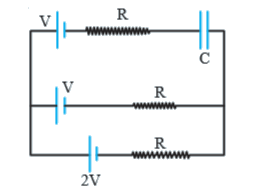
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
View SolutionFind charge on each capacitor and potential difference across each capacitor .

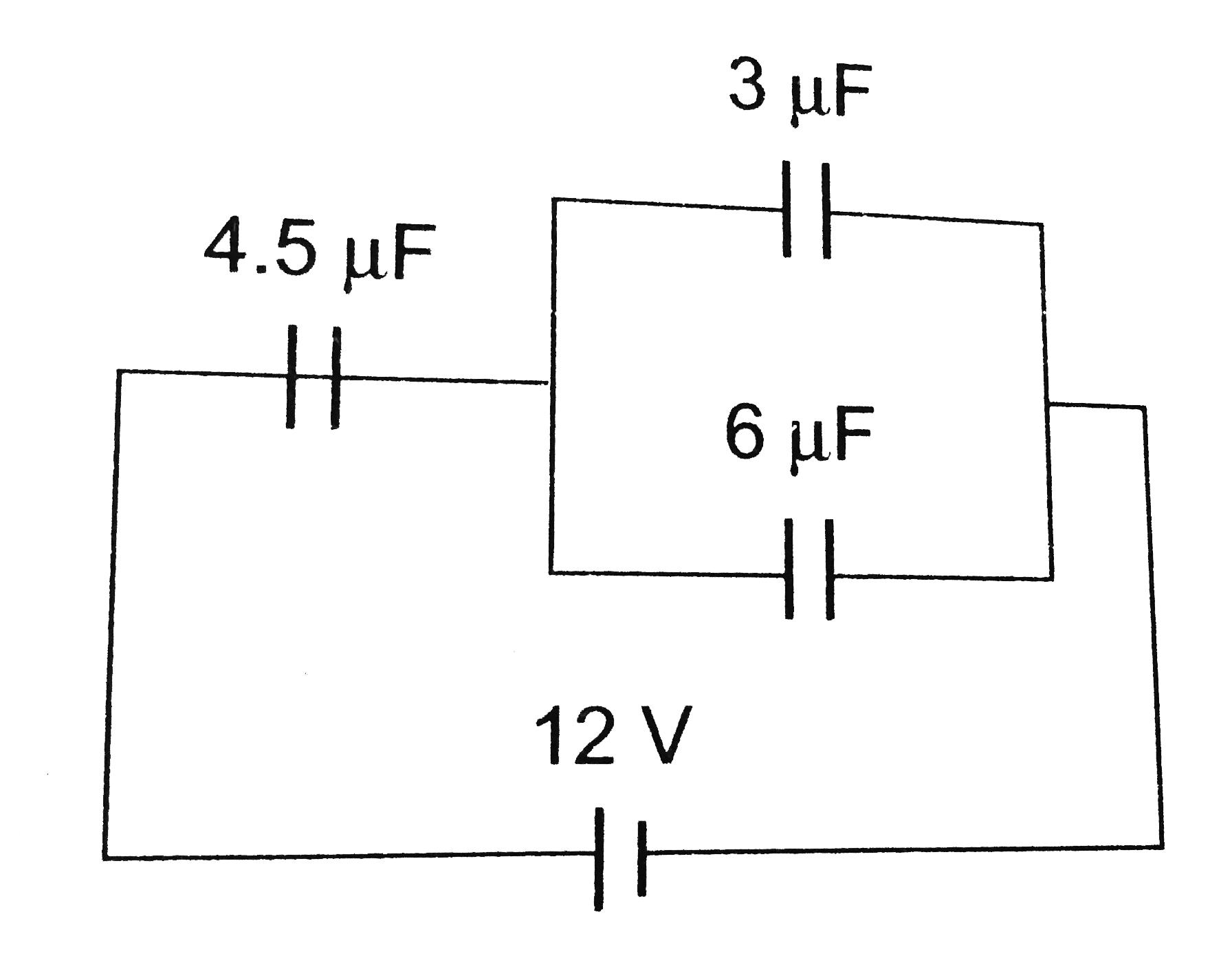
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
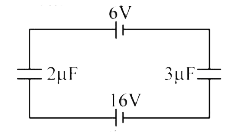
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
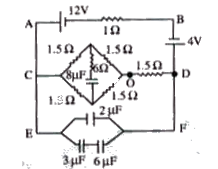
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA 220 V AC supply is connected between points A and B . What will be the potential difference V across the capacitor ?

View Solution
