In an inductor, the current / varies with time to l=5A+16.(A/s)t. If-induced emf in the induct is 5 mV, the self inductance of the inductor is
3.75X10−3H
3.75X10−4H
3.125X10−3H
3.125X10−4H
The correct Answer is:D
To find the self-inductance of the inductor given the current variation and the induced EMF, we can follow these steps:
1. Identify the given information:
- Current I(t)=5A+16A/s⋅t
- Induced EMF E=5mV=5×10−3V
2. Recall the formula for induced EMF in an inductor:
E=−LdIdt
where L is the self-inductance and dIdt is the rate of change of current with respect to time.
3. Differentiate the current with respect to time:
I(t)=5+16t
Taking the derivative:
dIdt=0+16=16A/s
4. Substitute the values into the EMF formula:
5×10−3=−L⋅16
5. Solve for L:
Rearranging the equation gives:
L=−5×10−316
Since self-inductance cannot be negative, we take the absolute value:
L=5×10−316
6. Calculate L:
L=516×10−3=0.3125×10−3H
7. Convert to standard form:
L=3.125×10−4H
Final Answer:
The self-inductance of the inductor is L=3.125×10−4H.
---
- Current I(t)=5A+16A/s⋅t
- Induced EMF E=5mV=5×10−3V
E=−LdIdt
where L is the self-inductance and dIdt is the rate of change of current with respect to time.
I(t)=5+16t
Taking the derivative:
dIdt=0+16=16A/s
5×10−3=−L⋅16
Rearranging the equation gives:
L=−5×10−316
Since self-inductance cannot be negative, we take the absolute value:
L=5×10−316
L=516×10−3=0.3125×10−3H
L=3.125×10−4H
The self-inductance of the inductor is L=3.125×10−4H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -C) Previous Years Questions
34 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
35 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
The current in ampere through an inductor is
i=(10+20t)
Here t is in second. The induced emf in the inductor 4V.
The self inductance of the indicator is, L…..H,
View SolutionA varying current ina coils changes from 10 A to zero in 0.5s .If the average emf induced in the coils is 220 V , the self- inductance of the coils is
View Solution
Knowledge Check
In a coil current falls from 5 A to 0 A in 0.2 s. If an average emf of 150 V is induced, then the self inductance of the coil is
A4HB2 HC3 HD6 H
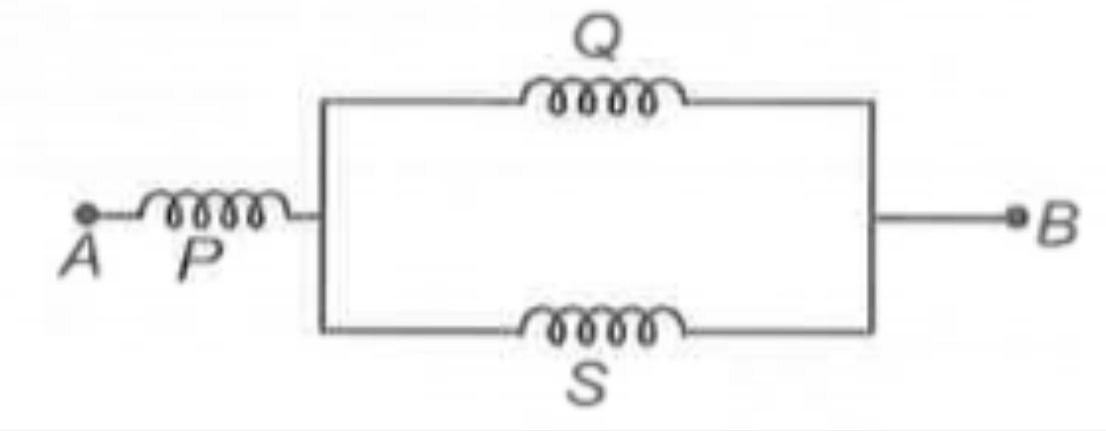
Three identical inductors are connected as shown in the figure. At the instant when current in inductor P is increasing at the rate of 0.0320 As−1 then magnitude of induced emf in it is 0.080 V. The equivalent inductance between the points A and B will be
View SolutionIf a current of 10 A changes in one second through a coil, and the induced emf is 20 V, then the self-inductance of the coil is
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionThe current (in Ampere) in an inductor is given by l=5+16t, where t in seconds. The selft - induced emf in it is 10mV. Find
(a) the self-inductance, and
(b) the energy stored in the inductor and the power supplied to it at t=1s
View SolutionIf a rate change of current of 4As−1 induces an emf of 20mV in a solenoid, what is the self inductance of the solenoid?
View SolutionWhen current in coil is uniformely reduced from 2A to 1A in 1 ms , the induced emf is 5V. The inductance of coil is :
View SolutionWhen the current in a certain inductor coil is 5.0A and is increasing at the rate of 10.0A/s,the magnitude of potential difference across the coil is 140V.When the current is 5.0A and decreasing at the rate of 10.0A/s,the potential difference is 60V.The self inductance of the coil is :
View Solution
