The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
12.5ms−2
7.5ms−2
5ms−2
2.5ms−2
The correct Answer is:A
To find the acceleration of the particle given that its velocity varies as v=5√x, we can follow these steps:
Step 1: Understand the relationship between acceleration, velocity, and displacement
Acceleration (a) can be expressed as the rate of change of velocity with respect to time:
a=dvdt
However, since velocity is also a function of displacement (x), we can use the chain rule to express acceleration in terms of displacement:
a=dvdt=dvdx⋅dxdt
Here, dxdt is the velocity (v) itself.
Step 2: Substitute the expression for velocity
From the problem, we know:
v=5√x
Thus, we can rewrite the acceleration as:
a=v⋅dvdx
Step 3: Differentiate the velocity with respect to displacement
Now, we need to find dvdx:
v=5√x=5x1/2
Differentiating v with respect to x:
dvdx=5⋅12x−1/2=52√x
Step 4: Substitute v and dvdx into the acceleration formula
Now we can substitute v and dvdx back into the acceleration equation:
a=v⋅dvdx=(5√x)⋅(52√x)
Step 5: Simplify the expression
Simplifying the expression, we have:
a=5√x⋅52√x=252=12.5m/s2
Final Result
Thus, the acceleration of the particle is:
12.5m/s2
---
Acceleration (a) can be expressed as the rate of change of velocity with respect to time:
a=dvdt
However, since velocity is also a function of displacement (x), we can use the chain rule to express acceleration in terms of displacement:
a=dvdt=dvdx⋅dxdt
Here, dxdt is the velocity (v) itself.
From the problem, we know:
v=5√x
Thus, we can rewrite the acceleration as:
a=v⋅dvdx
Now, we need to find dvdx:
v=5√x=5x1/2
Differentiating v with respect to x:
dvdx=5⋅12x−1/2=52√x
Now we can substitute v and dvdx back into the acceleration equation:
a=v⋅dvdx=(5√x)⋅(52√x)
Simplifying the expression, we have:
a=5√x⋅52√x=252=12.5m/s2
Thus, the acceleration of the particle is:
12.5m/s2
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.5
Explore 25 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.6
Explore 20 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:Check point 3.3
Explore 10 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEY ENGLISHChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V-t graph.
View SolutionThe velocity of particle moving in the positive direction of x axis varies as v=α√x, where α is a positive constnat. Assuming that at moment t=0, the particle was located at the point x=0. find.
(a) the time dependence of the velocity and the acceleration of the particle.
(b) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path
View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
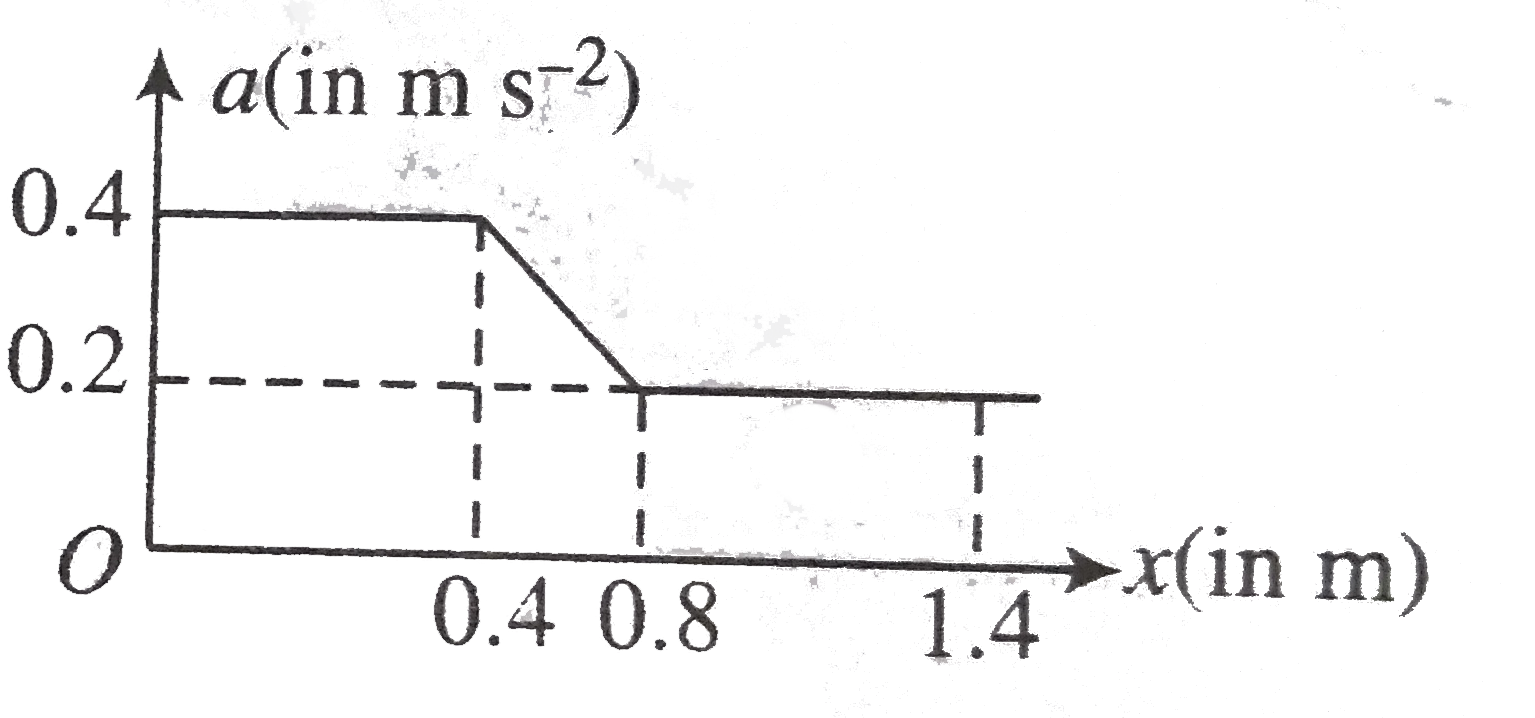
View SolutionVelocity of particle moving along positive x-direction is v=(40−10t)m/s. Here,t is in seconds. At time t=0, tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
View SolutionThe velocity of a particle defined by the relation v = 8 -0.02x, where v is expressed in m/s and x in meter. Knowing that x = 0 at t = 0, the acceleration at t=0 is
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View Solution
