The motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
4a
12a
6a
8a
The correct Answer is:D
To solve the problem, we need to find the distance traveled by a particle in the first 4 seconds, given that its motion is described by the equation u=At.
1. Identify the Given Information:
- The equation of motion is given as u=At.
- We need to find the distance traveled in the first 4 seconds.
2. Determine the Acceleration:
- The velocity u is a function of time t.
- To find the acceleration, we differentiate the velocity with respect to time:
a=dudt=d(At)dt=A
- Thus, the acceleration a is constant and equal to A.
3. Use the Equation of Motion:
- The equation for distance s traveled under constant acceleration is:
s=ut+12at2
- Here, u is the initial velocity, a is the acceleration, and t is the time.
4. Find the Initial Velocity:
- To find the initial velocity u at t=0:
u=A⋅0=0
- Therefore, the initial velocity u=0.
5. Substitute Values into the Equation:
- Now substitute u=0, a=A, and t=4 seconds into the equation:
s=0⋅4+12A(42)
- Simplifying this gives:
s=12A⋅16=8A
6. Conclusion:
- The distance traveled by the particle in the first 4 seconds is:
s=8A
Final Answer:
The distance traveled by the particle in the first 4 seconds is 8A.
---
- The equation of motion is given as u=At.
- We need to find the distance traveled in the first 4 seconds.
- The velocity u is a function of time t.
- To find the acceleration, we differentiate the velocity with respect to time:
a=dudt=d(At)dt=A
- Thus, the acceleration a is constant and equal to A.
- The equation for distance s traveled under constant acceleration is:
s=ut+12at2
- Here, u is the initial velocity, a is the acceleration, and t is the time.
- To find the initial velocity u at t=0:
u=A⋅0=0
- Therefore, the initial velocity u=0.
- Now substitute u=0, a=A, and t=4 seconds into the equation:
s=0⋅4+12A(42)
- Simplifying this gives:
s=12A⋅16=8A
- The distance traveled by the particle in the first 4 seconds is:
s=8A
The distance traveled by the particle in the first 4 seconds is 8A.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.5
25 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.6
20 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.3
10 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
The position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe potential energy (in SI units) of a particle of mass 2kg in a conservative field is U=6x−8y. If the initial velocity of the particle is →u=−1.5ˆi+2ˆj, then find the total distance travelled by the particle in the first two seconds.
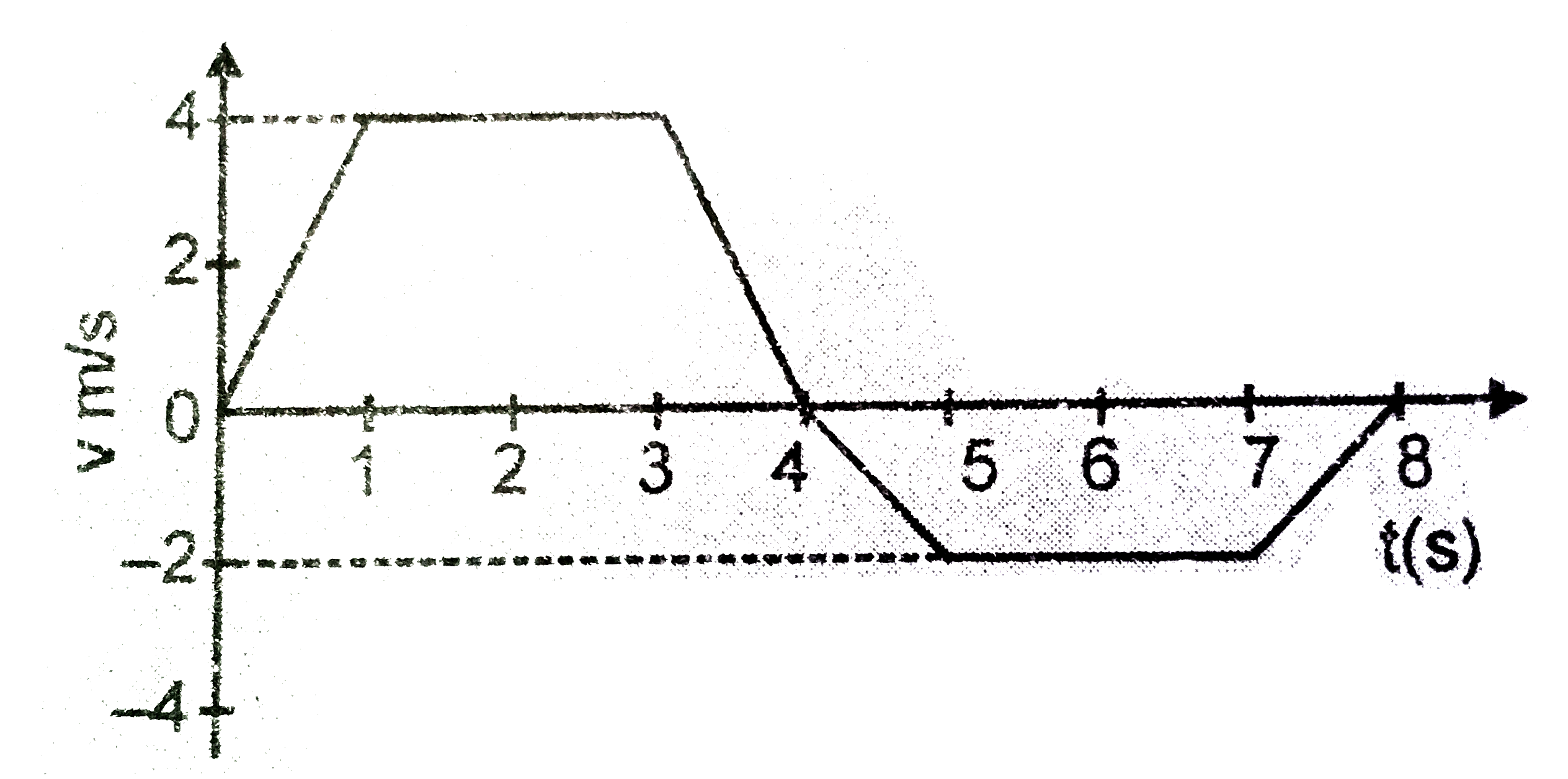
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
View SolutionVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
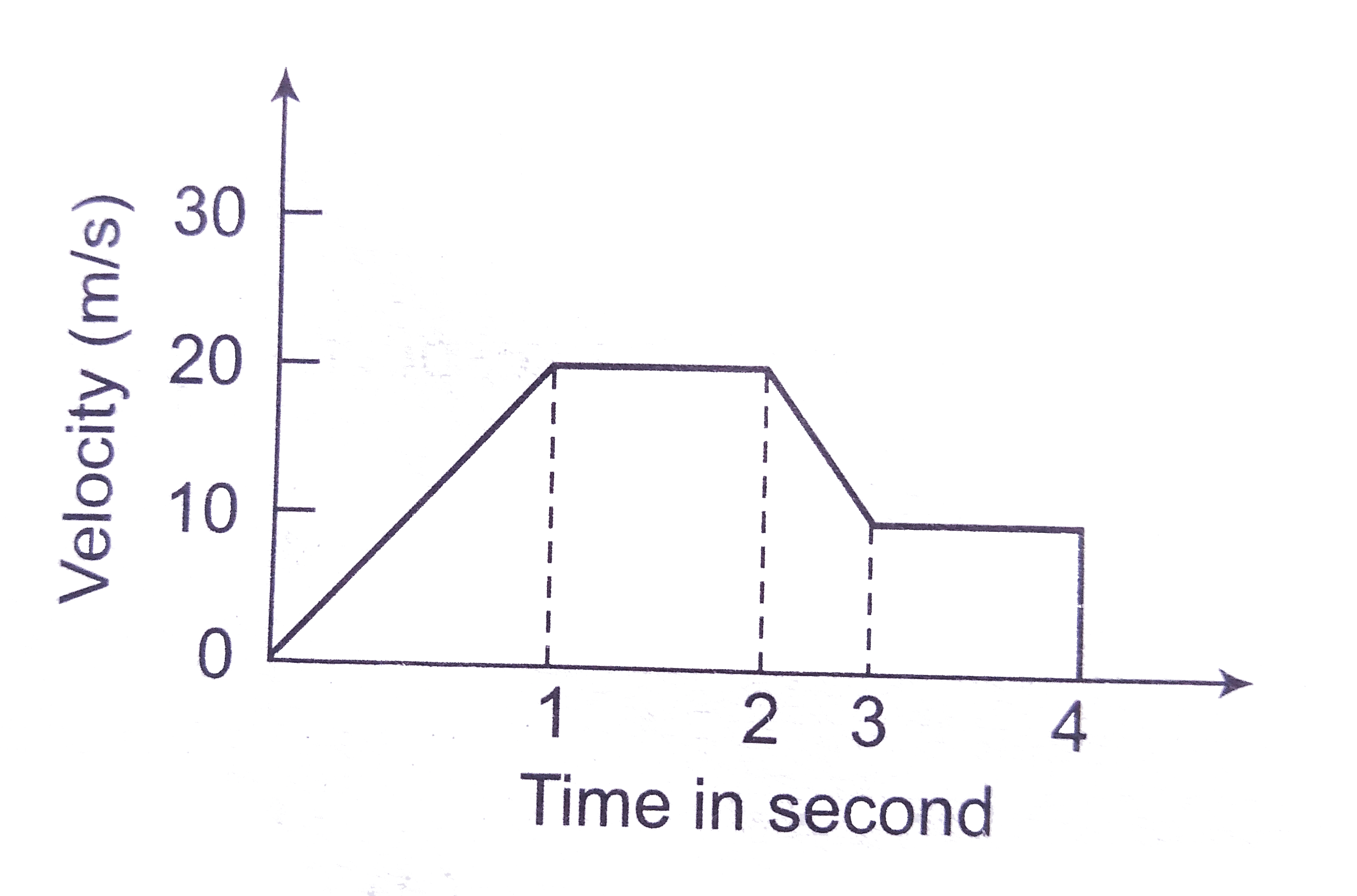
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q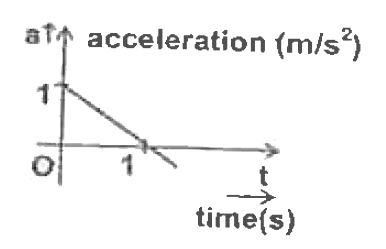
View SolutionA particle is dropped from the top of a high building 360 m. The distance travelled by the particle in ninth second is (g=10m/s2)
View SolutionA particle is moving in a striaght line and at a given time, its displacement is S=t3−6t2+9t, where t is in seconds and S is in meter . The total distance travelled by the particle during the first five seconds is
View SolutionA particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
View Solution
