Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
is constant
is increasing
is decreasing
first increases and then decreases
The correct Answer is:A
To find the force acting on a particle whose kinetic energy varies with time as K=4t2, we can follow these steps:
Step 1: Relate Kinetic Energy to Velocity
The kinetic energy K is given by the formula:
K=12mv2
Substituting the given expression for kinetic energy:
12mv2=4t2
Step 2: Solve for Velocity
Rearranging the equation to solve for v2:
mv2=8t2
v2=8t2m
Taking the square root of both sides gives:
v=√8t2m=2√2t√m
Step 3: Determine Acceleration
Since the velocity v is a function of time t, we can find the acceleration a by differentiating the velocity with respect to time:
a=dvdt=ddt(2√2t√m)=2√2√m
Step 4: Calculate Force
Using Newton's second law, the force F acting on the particle is given by:
F=ma
Substituting the expression for acceleration:
F=m(2√2√m)
Simplifying this gives:
F=2√2√m
Final Result
Thus, the force acting on the particle is:
F=2√2√m
---
The kinetic energy K is given by the formula:
K=12mv2
Substituting the given expression for kinetic energy:
12mv2=4t2
Rearranging the equation to solve for v2:
mv2=8t2
v2=8t2m
Taking the square root of both sides gives:
v=√8t2m=2√2t√m
Since the velocity v is a function of time t, we can find the acceleration a by differentiating the velocity with respect to time:
a=dvdt=ddt(2√2t√m)=2√2√m
Using Newton's second law, the force F acting on the particle is given by:
F=ma
Substituting the expression for acceleration:
F=m(2√2√m)
Simplifying this gives:
F=2√2√m
Thus, the force acting on the particle is:
F=2√2√m
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
The displacement of a particle of mass 2kg moving in a straight line varies with times as x=(2t3+2)m. Impulse of the force acting on the particle over a time interval between t = 0 and t = 1 s is
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionThe kinetic energy of a body moving along a straight line varies with time as shown in figure. The force acting on the body:
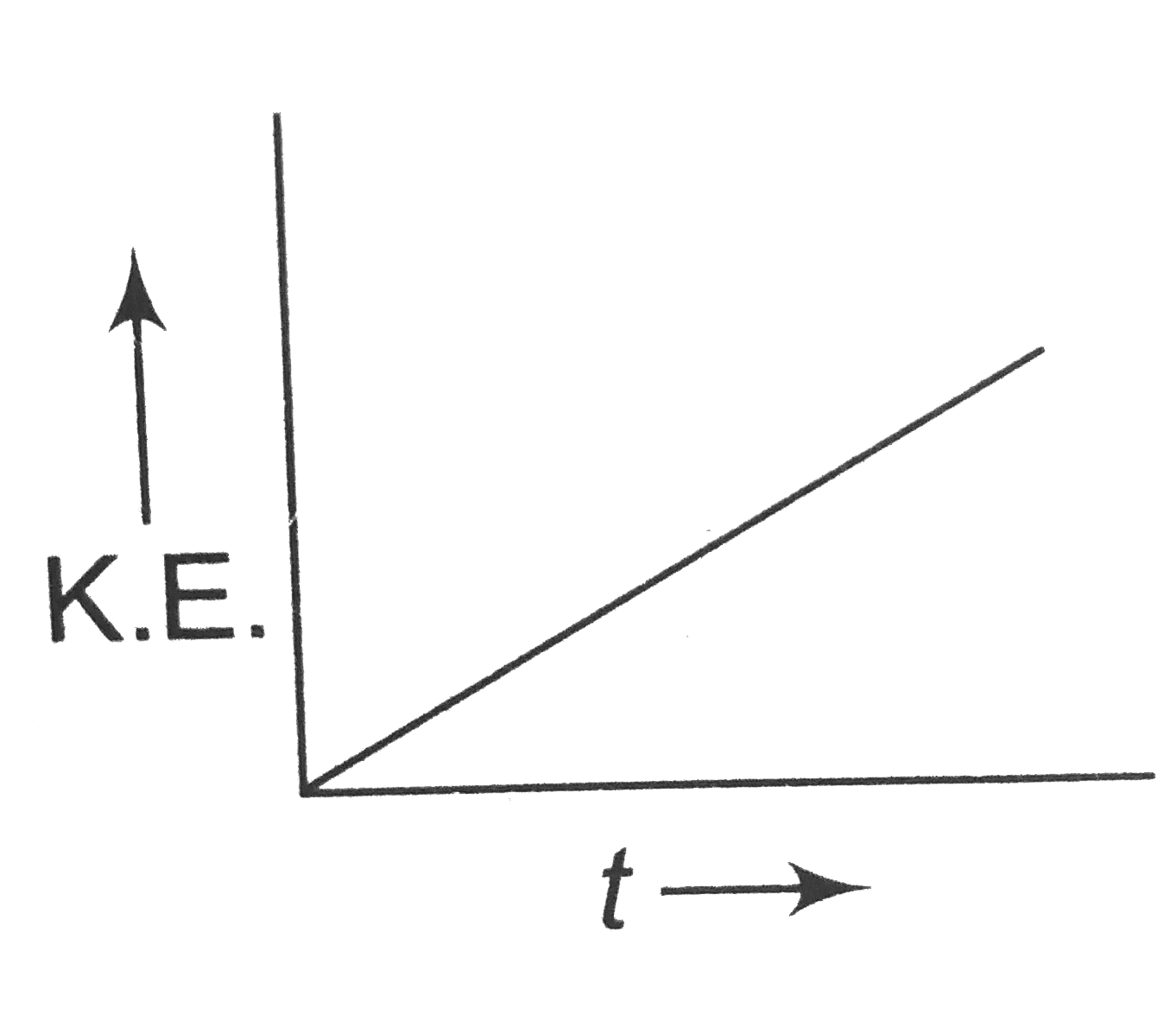
View SolutionThe coordinates of a particle moving in XY-plane vary with time as x=4t2,y=2t. The locus of the particle is a : -
View SolutionThe velocity time graph of a particle moving in a straight line is given line is given in the figure. Then starting from t=0, the particle
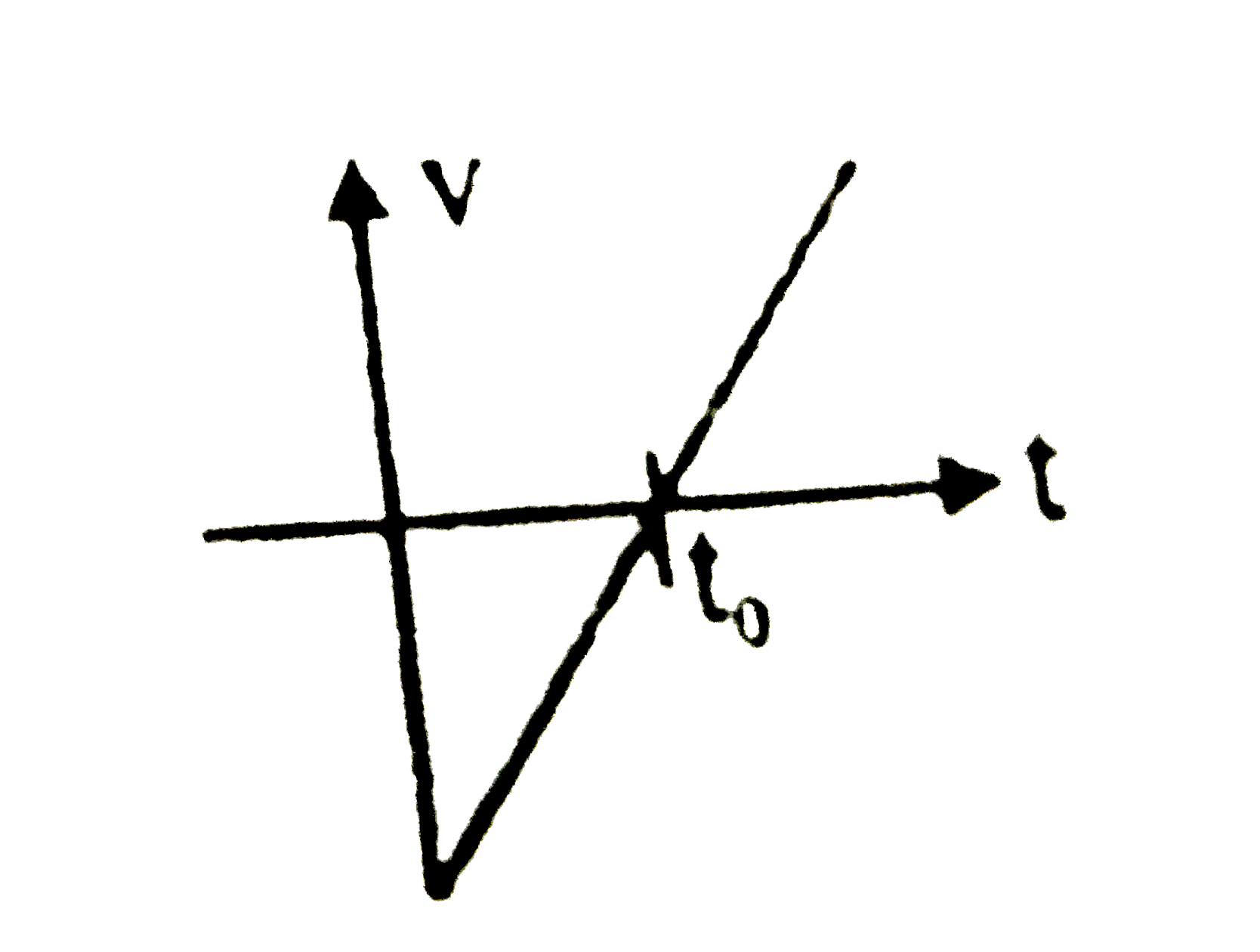
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionThe coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
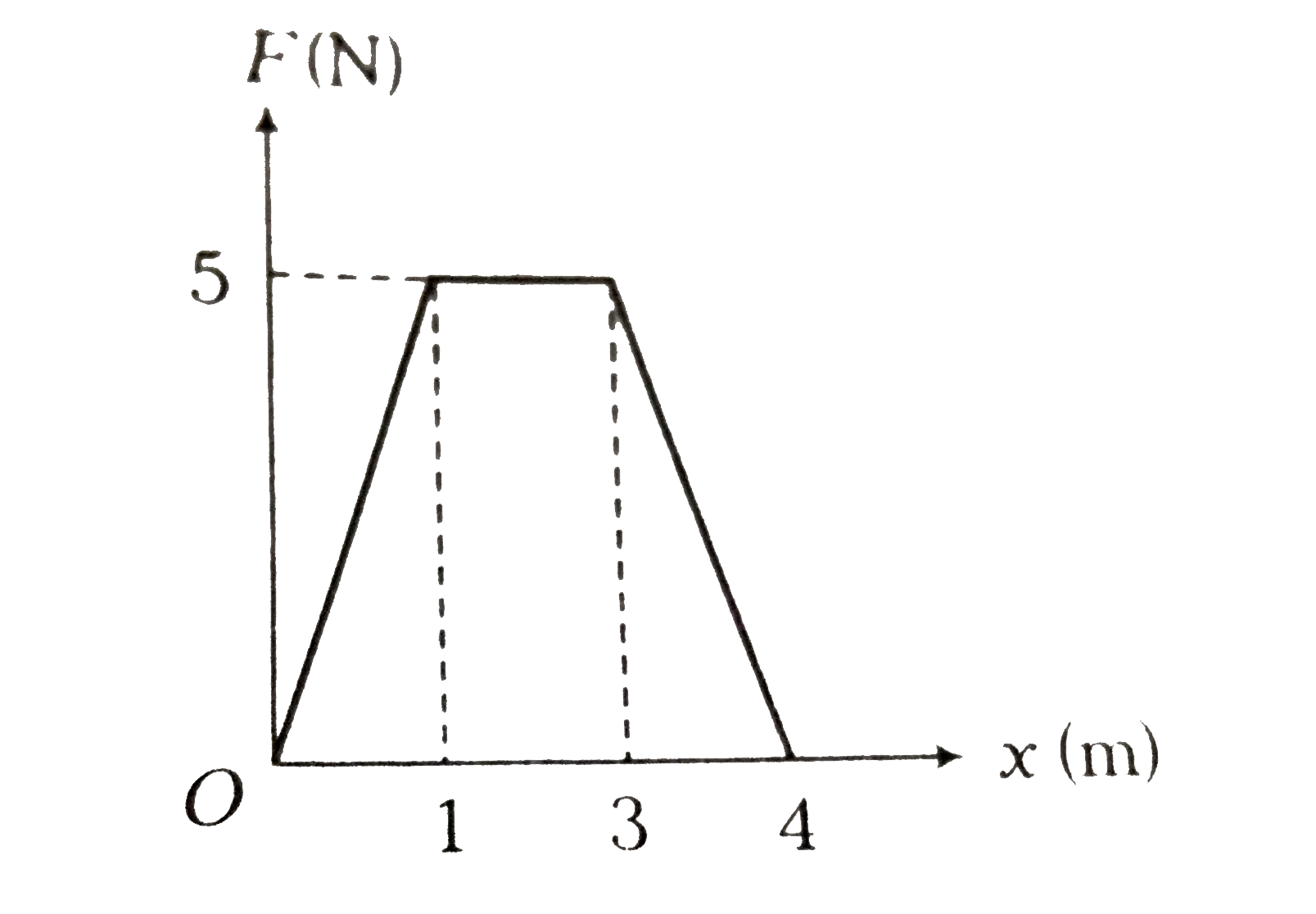
View SolutionThe net force acting on a particle moving along a straight line varies with time as shown in the diagram. Force is parallel to velocity. Which of the following graph is best representative of its speed with time? (Initial velocity of the particle is zero)
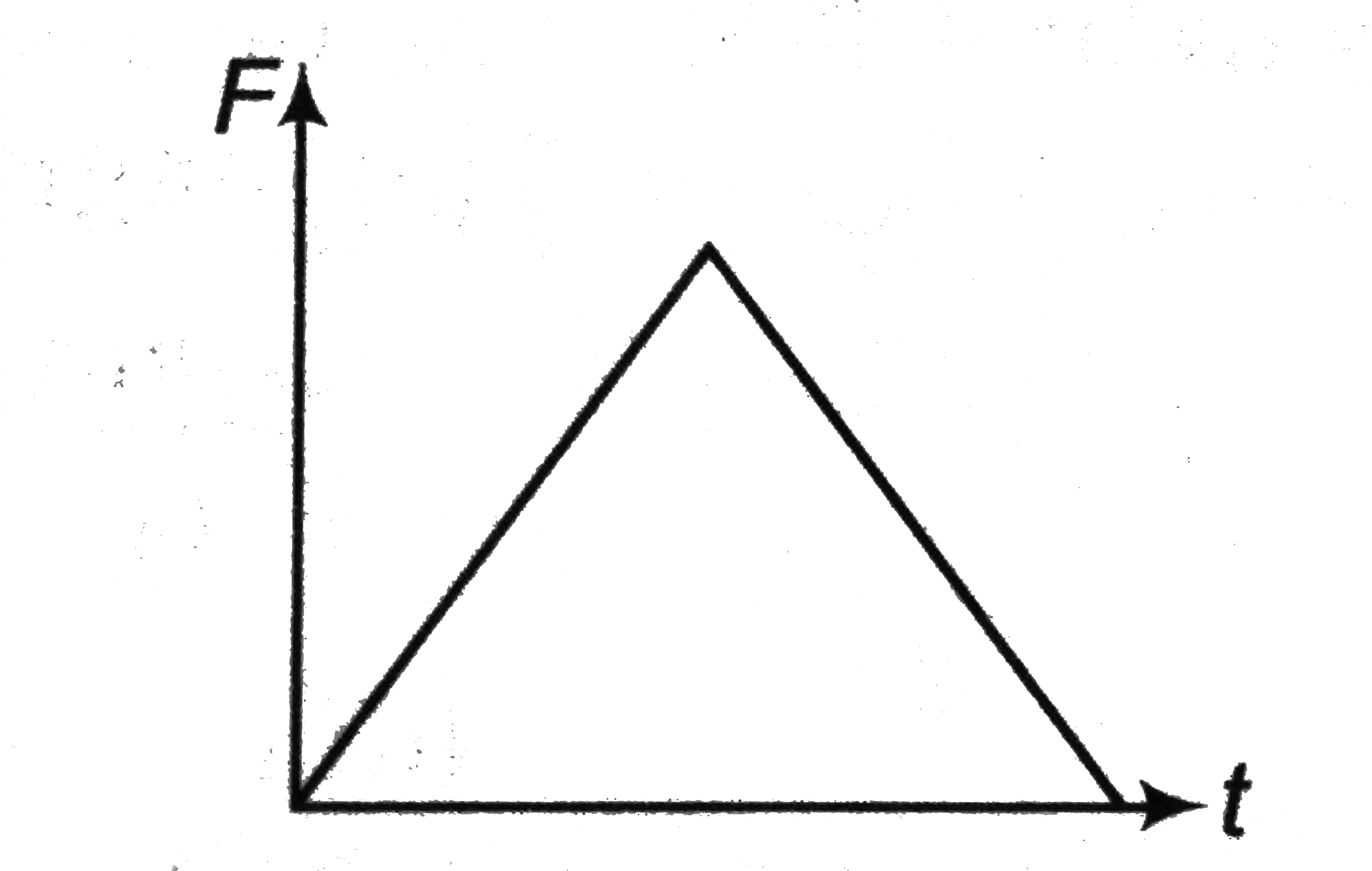
View Solution
