A solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be
(Force constant of the spring = 36 N/m)
√14m
√2.8m
√1.4m
√0.7m
The correct Answer is:B
To solve the problem, we need to find the maximum compression of the spring when a solid sphere collides with it. We will use the principles of conservation of energy.
1. Identify the Given Values:
- Mass of the sphere, m=2kg
- Initial velocity of the sphere, v=6m/s
- Spring constant, k=36N/m
2. Calculate the Initial Kinetic Energy:
The sphere has both translational and rotational kinetic energy. However, since it is rolling without slipping, we can express the total kinetic energy as:
KEinitial=KEtranslational+KErotational
The translational kinetic energy is given by:
KEtranslational=12mv2
The moment of inertia I for a solid sphere is:
I=25mr2
The angular velocity ω can be related to the linear velocity v by:
v=rω⟹ω=vr
Thus, the rotational kinetic energy is:
KErotational=12Iω2=12(25mr2)(v2r2)=15mv2
Therefore, the total kinetic energy becomes:
KEinitial=12mv2+15mv2=(510+210)mv2=710mv2
3. Substitute the Values:
KEinitial=710×2kg×(6m/s)2=710×2×36=7×7210=50.4J
4. Set Up the Energy Conservation Equation:
At maximum compression x, all kinetic energy is converted into potential energy stored in the spring:
KEinitial=PEspring⟹12kx2
Thus, we have:
50.4=12×36×x2
5. Solve for x:
Rearranging gives:
50.4=18x2⟹x2=50.418=2.8⟹x=√2.8≈1.673m
6. Final Result:
The maximum compression produced in the spring is approximately:
x≈1.673m
- Mass of the sphere, m=2kg
- Initial velocity of the sphere, v=6m/s
- Spring constant, k=36N/m
The sphere has both translational and rotational kinetic energy. However, since it is rolling without slipping, we can express the total kinetic energy as:
KEinitial=KEtranslational+KErotational
The translational kinetic energy is given by:
KEtranslational=12mv2
The moment of inertia I for a solid sphere is:
I=25mr2
The angular velocity ω can be related to the linear velocity v by:
v=rω⟹ω=vr
Thus, the rotational kinetic energy is:
KErotational=12Iω2=12(25mr2)(v2r2)=15mv2
Therefore, the total kinetic energy becomes:
KEinitial=12mv2+15mv2=(510+210)mv2=710mv2
KEinitial=710×2kg×(6m/s)2=710×2×36=7×7210=50.4J
At maximum compression x, all kinetic energy is converted into potential energy stored in the spring:
KEinitial=PEspring⟹12kx2
Thus, we have:
50.4=12×36×x2
Rearranging gives:
50.4=18x2⟹x2=50.418=2.8⟹x=√2.8≈1.673m
The maximum compression produced in the spring is approximately:
x≈1.673m
Similar Questions
A solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
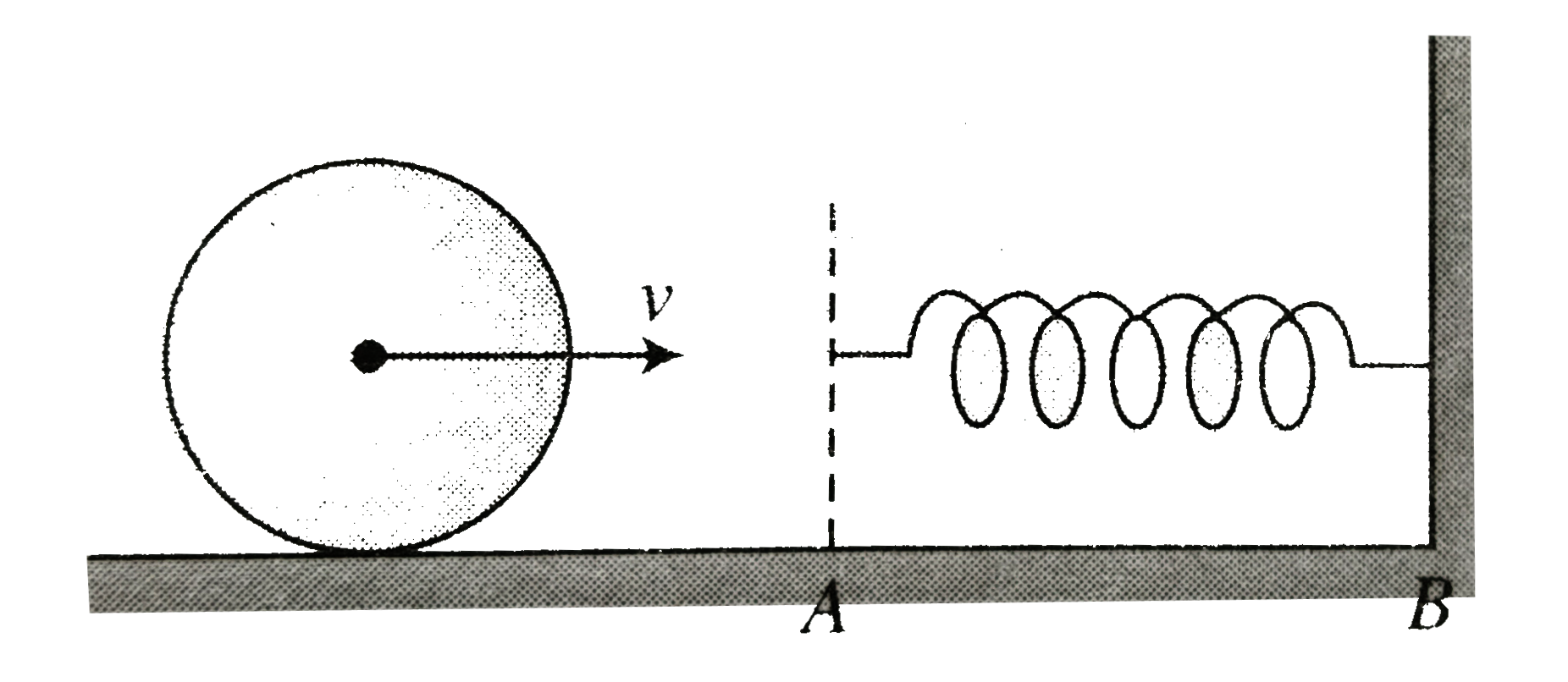
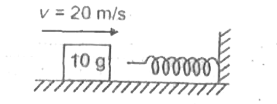
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

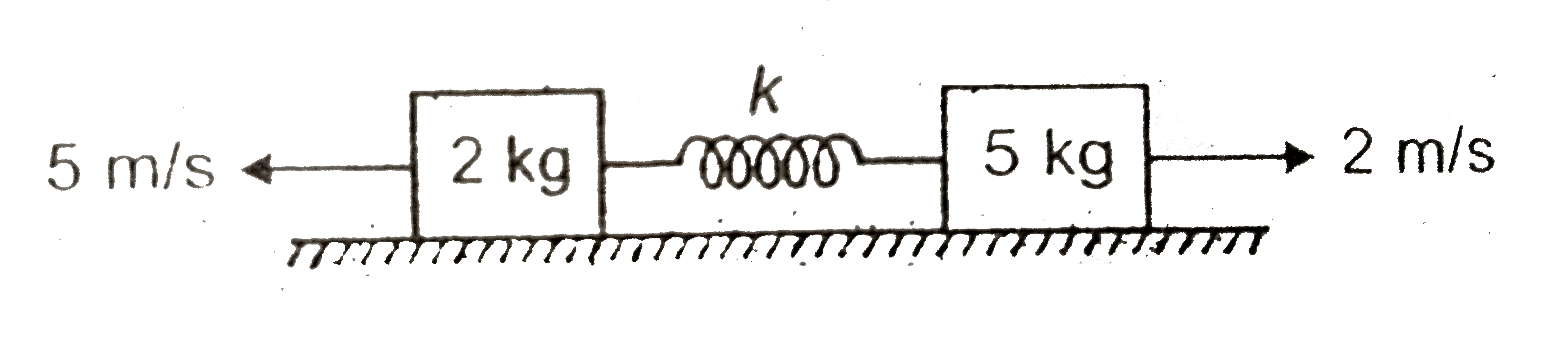
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View Solution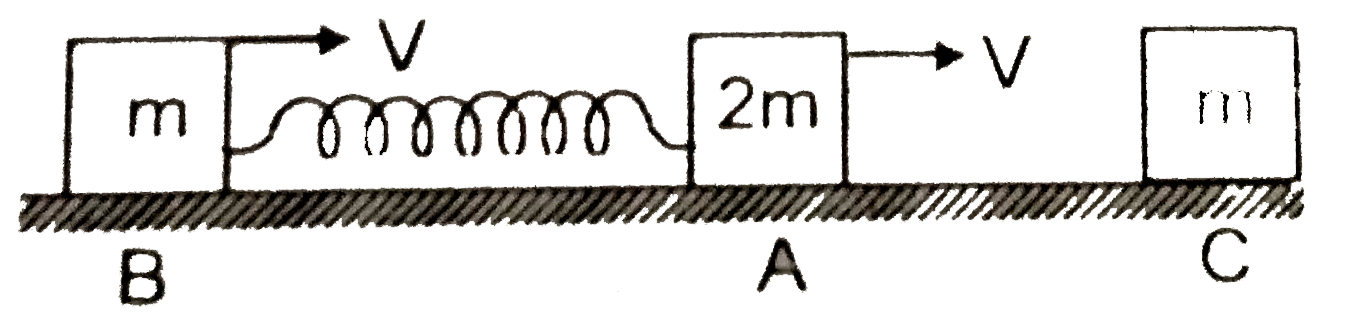
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be
View Solution
