A 2 kg block slides on a horizontal floor with a speed of 4 m/s. It strikes an uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is 15 N and spring constant is 10000 N/m. The spring is compressed by (in cm):
(a)2.5
(b)
(c)
(d)
The correct Answer is:D
To solve the problem step-by-step, we will use the concepts of energy conservation and work done against friction.
Step 1: Identify the Given Data
- Mass of the block (m) = 2 kg
- Initial speed of the block (v) = 4 m/s
- Kinetic friction force (F_friction) = 15 N
- Spring constant (k) = 10,000 N/m
Step 2: Calculate the Initial Kinetic Energy (KE)
The kinetic energy of the block can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×2kg×(4m/s)2=12×2×16=16J
Step 3: Set Up the Energy Conservation Equation
When the block compresses the spring, the kinetic energy is converted into the potential energy of the spring and the work done against friction. The equation can be set up as:
KE=PE+W
Where:
- PE=12kx2 (Potential energy of the spring)
- W=Ffriction⋅x (Work done against friction)
So, we have:
16=12kx2+Ffriction⋅x
Step 4: Substitute the Known Values
Substituting the values of k and Ffriction:
16=12×10000N/m⋅x2+15N⋅x
This simplifies to:
16=5000x2+15x
Step 5: Rearrange the Equation
Rearranging the equation gives us a standard quadratic form:
5000x2+15x−16=0
Step 6: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a, where a=5000, b=15, and c=−16:
1. Calculate the discriminant:
D=b2−4ac=152−4×5000×(−16)=225+320000=320225
2. Calculate x:
x=−15±√3202252×5000
x=−15±566.310000
Taking the positive root:
x=551.310000=0.05513m
Step 7: Convert to Centimeters
To convert meters to centimeters:
x=0.05513m×100=5.513cm
Final Answer
The spring is compressed by approximately 5.5 cm.
---
- Mass of the block (m) = 2 kg
- Initial speed of the block (v) = 4 m/s
- Kinetic friction force (F_friction) = 15 N
- Spring constant (k) = 10,000 N/m
The kinetic energy of the block can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×2kg×(4m/s)2=12×2×16=16J
When the block compresses the spring, the kinetic energy is converted into the potential energy of the spring and the work done against friction. The equation can be set up as:
KE=PE+W
Where:
- PE=12kx2 (Potential energy of the spring)
- W=Ffriction⋅x (Work done against friction)
16=12kx2+Ffriction⋅x
Substituting the values of k and Ffriction:
16=12×10000N/m⋅x2+15N⋅x
This simplifies to:
16=5000x2+15x
Rearranging the equation gives us a standard quadratic form:
5000x2+15x−16=0
Using the quadratic formula x=−b±√b2−4ac2a, where a=5000, b=15, and c=−16:
1. Calculate the discriminant:
D=b2−4ac=152−4×5000×(−16)=225+320000=320225
2. Calculate x:
x=−15±√3202252×5000
x=−15±566.310000
Taking the positive root:
x=551.310000=0.05513m
To convert meters to centimeters:
x=0.05513m×100=5.513cm
The spring is compressed by approximately 5.5 cm.
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE)
Explore 80 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
Explore 5 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA body of mass m=3.90 kg slides on a horizontal frictionless table with a speed of v=120 ms−1. It is brought to rest in compressing a spring in its path. How much does spring is compressed, if its force constant k is 135 Nm−1?
View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionA block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
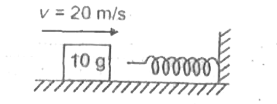
View SolutionA block of mass 2.0 kg is given an initial speed along the floor towards a spring as shown. The coefficient of kinetic friction between the floor and the block is 0.4 and force constant of the spring is 5.6×103 N/m. The block compresses the spring by 10cm before it stops for a moment. What is the initial speed (m/s) of the block?

View SolutionA 3.0kg block slides on a frictionless horizontal surface, first moving to the left at 50m/s. It collides with a spring as it moves left, compresses the spring and is brought to rest momentarily. The body continues to be accelerated to the right by the force of compressed spring. Finally, the body moves to the right at 40m/s. The block remains in contact with the spring for 0.020s. What were the magnitude and direction of the impulse of the spring on the block? What was the spring's average force on the block?
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View Solution