The relation between acceleration and displacement of four particles are given below. The particle undergoing SHM is:
ax=+2x
ax=+2x2
ax=−2x2
ax=−2x
The correct Answer is:D
To determine which particle is undergoing simple harmonic motion (SHM) based on the given relations between acceleration (a) and displacement (x), we can analyze the provided equations step by step.
1. Understanding the Relation of Acceleration and Displacement:
- In SHM, the acceleration (a) is directly proportional to the displacement (x) and is always directed towards the mean position. This can be mathematically expressed as:
a=−kx
where k is a positive constant.
2. Analyzing Each Given Option:
- We have four options for the relation between acceleration and displacement:
1. ax=+2x
2. ax=+2x2
3. ax=−2x2
4. ax=−2x
3. Identifying the Correct Form:
- For SHM, we need a to be proportional to x with a negative sign. This means we are looking for a relation of the form a=−kx.
4. Evaluating Each Option:
- Option 1: ax=+2x
- This is positive and does not represent SHM.
- Option 2: ax=+2x2
- This is also positive and not linear in x, hence does not represent SHM.
- Option 3: ax=−2x2
- This is negative but not linear in x (it has x2), hence does not represent SHM.
- Option 4: ax=−2x
- This is negative and linear in x, which matches the condition for SHM.
5. Conclusion:
- The particle undergoing simple harmonic motion is described by the equation:
ax=−2x
Therefore, the correct answer is Option 4.
- In SHM, the acceleration (a) is directly proportional to the displacement (x) and is always directed towards the mean position. This can be mathematically expressed as:
a=−kx
where k is a positive constant.
- We have four options for the relation between acceleration and displacement:
1. ax=+2x
2. ax=+2x2
3. ax=−2x2
4. ax=−2x
- For SHM, we need a to be proportional to x with a negative sign. This means we are looking for a relation of the form a=−kx.
- Option 1: ax=+2x
- This is positive and does not represent SHM.
- Option 2: ax=+2x2
- This is also positive and not linear in x, hence does not represent SHM.
- Option 3: ax=−2x2
- This is negative but not linear in x (it has x2), hence does not represent SHM.
- Option 4: ax=−2x
- This is negative and linear in x, which matches the condition for SHM.
- The particle undergoing simple harmonic motion is described by the equation:
ax=−2x
Therefore, the correct answer is Option 4.
Similar Questions
Knowledge Check
- Question 1 - Select One
The ralation between acceleration and displacement of four particles are given below
which one of the particles is executing simple harmonic motion?Aax=+2xBax=+2x2Cax=−2x2Dax=−2x - Question 2 - Select One
Which of the following relationships between the acceleration a and the displacement x of a particle executing simple harmonic motion?
Aa=2x2Ba=−2x2Ca=2xDa=−2x
The relation between position (x) and time (t) are given below for a particle moving along a straight line. Which of the following equation represents uniformly accelerated motion? [where αandβ are positive constants]
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
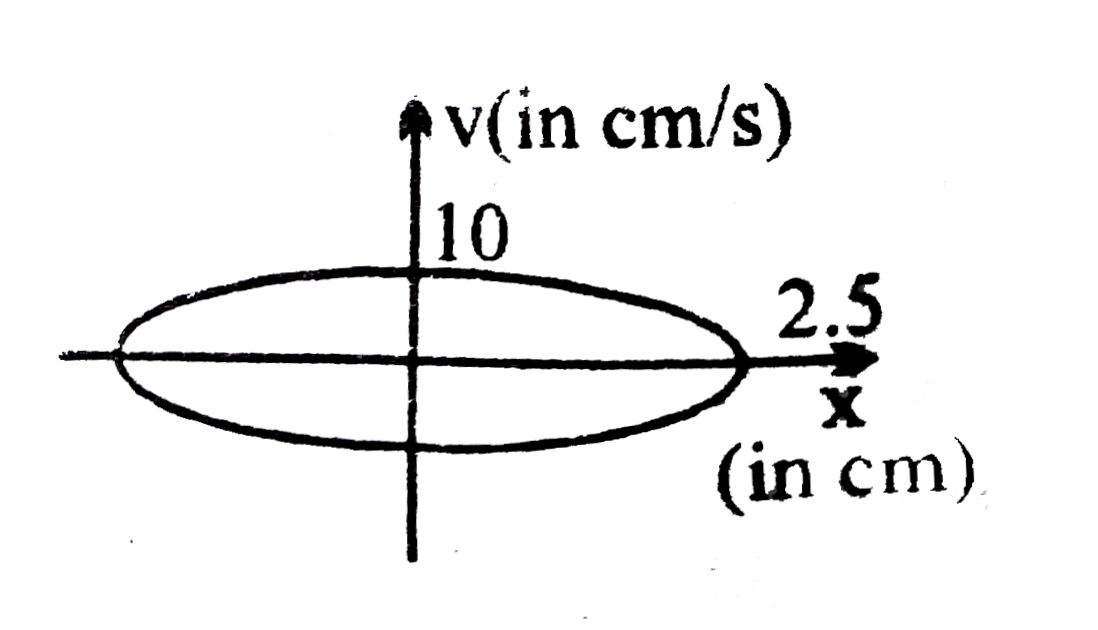 View Solution
View SolutionThe displacement-time graph of a particle is as shown below. It indicates that
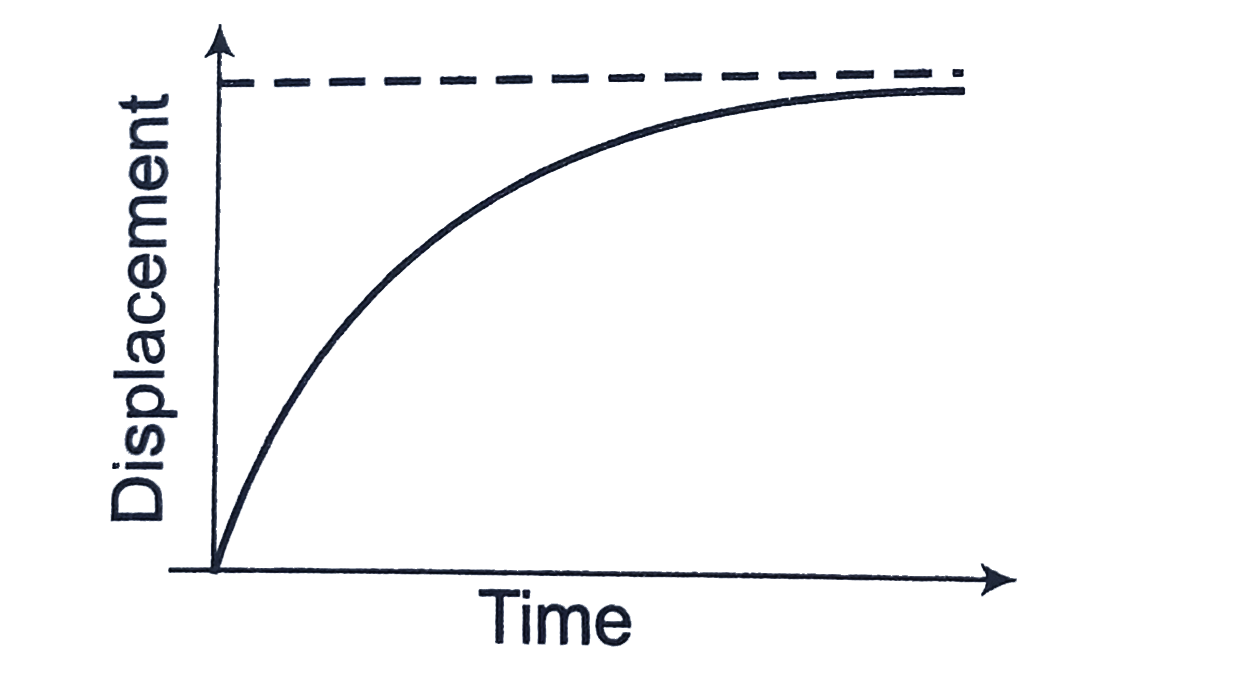 View Solution
View SolutionDraw the graph between displacement and
potential energy for a particle executing SHM.View SolutionThe graph between displacement and time for a particle moving with uniform acceleration is a
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View Solution

