Draw the graph between displacement and
potential energy for a particle executing SHM.
To draw the graph between displacement and potential energy for a particle executing Simple Harmonic Motion (SHM), we can follow these steps:
Step 1: Understand the relationship between potential energy and displacement
The potential energy (PE) of a particle in SHM is given by the formula:
PE=12mω2x2
where:
- m is the mass of the particle,
- ω is the angular frequency,
- x is the displacement from the mean position.
Step 2: Identify the nature of the relationship
From the formula, we can see that potential energy is directly proportional to the square of the displacement (x2). This means that as displacement increases, potential energy increases quadratically.
Step 3: Determine the graph shape
Since the relationship is quadratic (PE∝x2), the graph between potential energy and displacement will be a parabola opening upwards.
Step 4: Identify the maximum potential energy
The maximum displacement in SHM is denoted as A (the amplitude). Thus, the maximum potential energy can be calculated as:
PEmax=12mω2A2
Step 5: Draw the graph
1. On the x-axis, plot the displacement x.
2. On the y-axis, plot the potential energy PE.
3. The graph will start from the origin (0,0) and will curve upwards, forming a parabola. The vertex of the parabola is at the origin, and it will reach its maximum value at x=A.
Step 6: Label the graph
Label the axes as follows:
- X-axis: Displacement (x)
- Y-axis: Potential Energy (PE)
- Mark the maximum potential energy point at x=A.
Final Graph Representation
The graph will look like a parabola starting from the origin (0,0) and curving upwards, peaking at the maximum potential energy value when x=A.
---
The potential energy (PE) of a particle in SHM is given by the formula:
PE=12mω2x2
where:
- m is the mass of the particle,
- ω is the angular frequency,
- x is the displacement from the mean position.
From the formula, we can see that potential energy is directly proportional to the square of the displacement (x2). This means that as displacement increases, potential energy increases quadratically.
Since the relationship is quadratic (PE∝x2), the graph between potential energy and displacement will be a parabola opening upwards.
The maximum displacement in SHM is denoted as A (the amplitude). Thus, the maximum potential energy can be calculated as:
PEmax=12mω2A2
1. On the x-axis, plot the displacement x.
2. On the y-axis, plot the potential energy PE.
3. The graph will start from the origin (0,0) and will curve upwards, forming a parabola. The vertex of the parabola is at the origin, and it will reach its maximum value at x=A.
Label the axes as follows:
- X-axis: Displacement (x)
- Y-axis: Potential Energy (PE)
- Mark the maximum potential energy point at x=A.
The graph will look like a parabola starting from the origin (0,0) and curving upwards, peaking at the maximum potential energy value when x=A.
Similar Questions
Draw the graph between displacement and
total energy for a particle executing SHM.
View SolutionDraw the graph between displacement and
kinetic energy for a particle executing SHM.
View SolutionEnergy of particle executing SHM depends upon
View SolutionWrite the relation between acceleration, displacement and frequency of a particle executing SHM.
View SolutionDraw a graph between displacement and time for a body executing natural vibrations.
View SolutionDraw a graph between displacement from mean position and time for a body executing free vibration in a vacuum.
View SolutionThe ration of kinetic energy to the potential energy of a particle executing SHM at a distance equal to half its amplitude , the distance being measured from its equilibrium position is
View SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
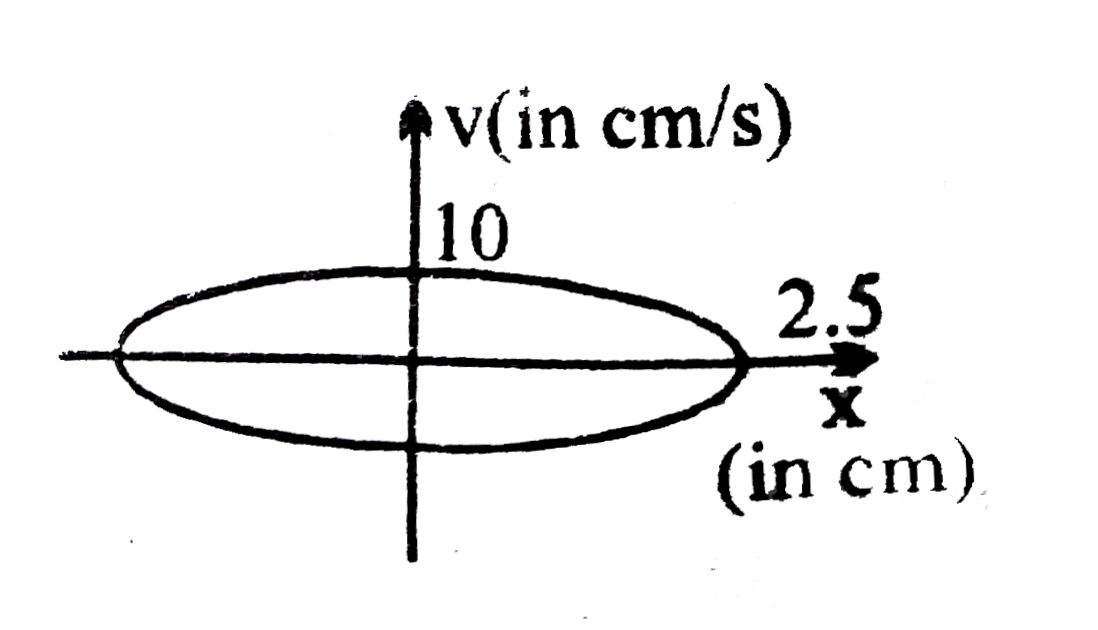
View Solution
