The relation between position (x) and time (t) are given below for a particle moving along a straight line. Which of the following equation represents uniformly accelerated motion? [where αandβ are positive constants]
βx=αt+αβ
αx=β+t
xt=αβ
αt=√β+x
The correct Answer is:D
To determine which of the given equations represents uniformly accelerated motion, we need to analyze each option based on the characteristics of uniformly accelerated motion. In uniformly accelerated motion, the position x as a function of time t can be expressed in a quadratic form, typically represented by the equation:
x=ut+12at2
where u is the initial velocity and a is the constant acceleration.
Now, let's analyze each option:
1. Option 1: βx=αt+αβ
Rearranging gives:
x=αβt+β
This is a linear equation in t and does not represent uniformly accelerated motion.
2. Option 2: αx=β+t
Rearranging gives:
x=βα+1αt
This is also a linear equation in t and does not represent uniformly accelerated motion.
3. Option 3: xt=αβ
Rearranging gives:
x=αβt
This indicates an inverse relationship between x and t, which does not represent uniformly accelerated motion.
4. Option 4: αt=√β+x
Squaring both sides gives:
(αt)2=β+x
Rearranging gives:
x=(αt)2−β
This is a quadratic equation in t, which indicates that x is proportional to t2, characteristic of uniformly accelerated motion.
Based on this analysis, the equation that represents uniformly accelerated motion is:
αt=√β+x
x=αβt+β
This is a linear equation in t and does not represent uniformly accelerated motion.
x=βα+1αt
This is also a linear equation in t and does not represent uniformly accelerated motion.
x=αβt
This indicates an inverse relationship between x and t, which does not represent uniformly accelerated motion.
(αt)2=β+x
Rearranging gives:
x=(αt)2−β
This is a quadratic equation in t, which indicates that x is proportional to t2, characteristic of uniformly accelerated motion.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
58 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
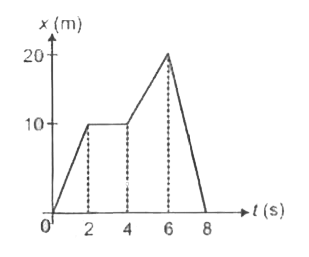
The position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionWhich of the following relations representing displacement x (t) of particle describes motion with constant acceleration?
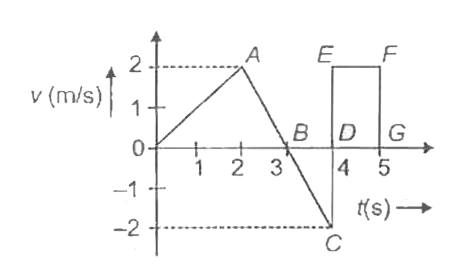
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
View SolutionFor which of the following graphs the average velocity of a particle moving along a straight line for time interval (0,t) must be negative−
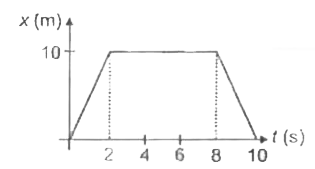
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
View SolutionFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
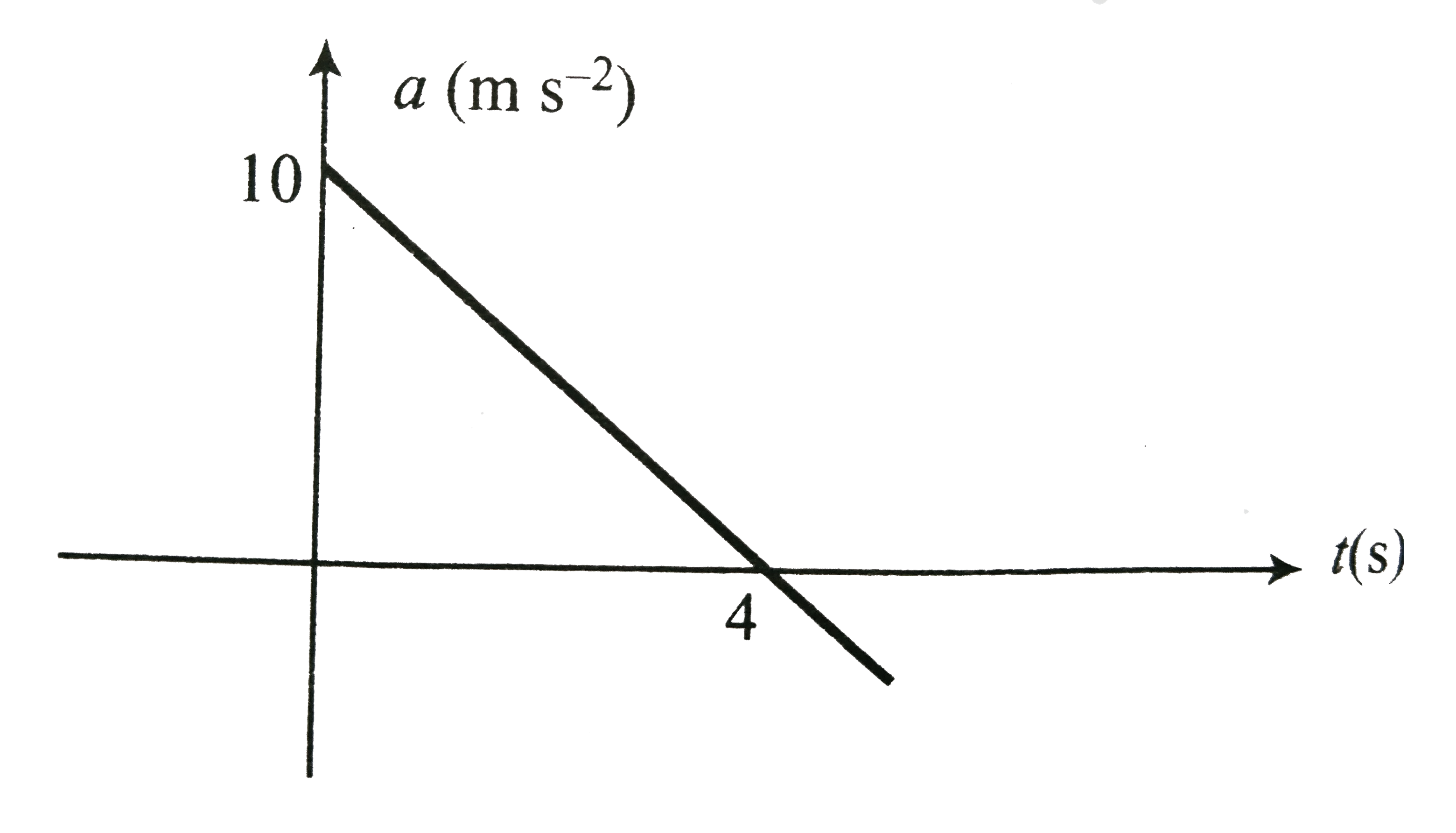
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View Solution
