Assertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
To solve the assertion and reason question regarding the spring-block system, we will break down the problem step by step.
Step 1: Understand the Assertion and Reason
- Assertion: If the length of the spring and the mass of the block are both halved, then the angular frequency of oscillations will remain unchanged.
- Reason: Angular frequency is given by the formula ω=√km.
Step 2: Analyze the Angular Frequency Formula
The angular frequency ω is defined as:
ω=√km
where k is the spring constant and m is the mass of the block.
Step 3: Determine the Effect of Halving the Length of the Spring
- The spring constant k is inversely proportional to the natural length of the spring. If the length of the spring is halved, the spring constant will double:
k′=2k
where k′ is the new spring constant after halving the length.
Step 4: Determine the Effect of Halving the Mass
- If the mass of the block is halved, the new mass will be:
m′=m2
Step 5: Calculate the New Angular Frequency
Now, substituting the new values of k and m into the angular frequency formula:
ω′=√k′m′=√2km2=√2k⋅2m=√4km=2√km=2ω
Step 6: Conclusion
From the calculations, we find that the new angular frequency ω′ is double the original angular frequency ω:
ω′=2ω
Thus, the assertion that the angular frequency remains unchanged is false. The reason that angular frequency is given by ω=√km is true.
Final Answer
- Assertion: False
- Reason: True
- Therefore, the correct option is that the assertion is false, and the reason is true.
---
- Assertion: If the length of the spring and the mass of the block are both halved, then the angular frequency of oscillations will remain unchanged.
- Reason: Angular frequency is given by the formula ω=√km.
The angular frequency ω is defined as:
ω=√km
where k is the spring constant and m is the mass of the block.
- The spring constant k is inversely proportional to the natural length of the spring. If the length of the spring is halved, the spring constant will double:
k′=2k
where k′ is the new spring constant after halving the length.
- If the mass of the block is halved, the new mass will be:
m′=m2
Now, substituting the new values of k and m into the angular frequency formula:
ω′=√k′m′=√2km2=√2k⋅2m=√4km=2√km=2ω
From the calculations, we find that the new angular frequency ω′ is double the original angular frequency ω:
ω′=2ω
Thus, the assertion that the angular frequency remains unchanged is false. The reason that angular frequency is given by ω=√km is true.
- Assertion: False
- Reason: True
- Therefore, the correct option is that the assertion is false, and the reason is true.
Similar Questions
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
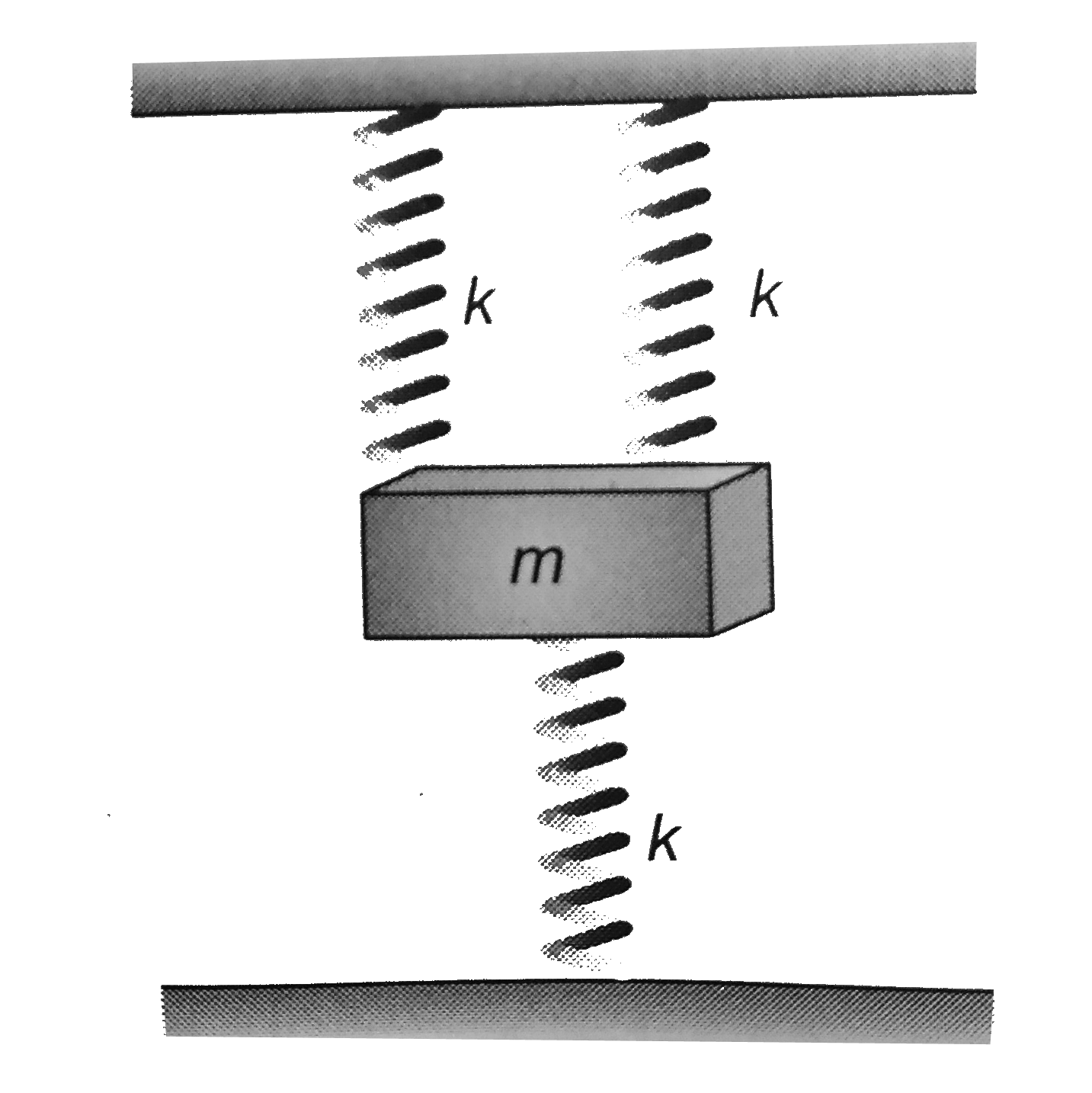
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionTwo equal masses are connected by a spring satisfying Hook's law and are placed on a frictionless table. The spring is elongated a little and allowed to go. Let the angular frequency of oscillations be ω. Now one of the masses is stopped. The square of the new angular frequency is :
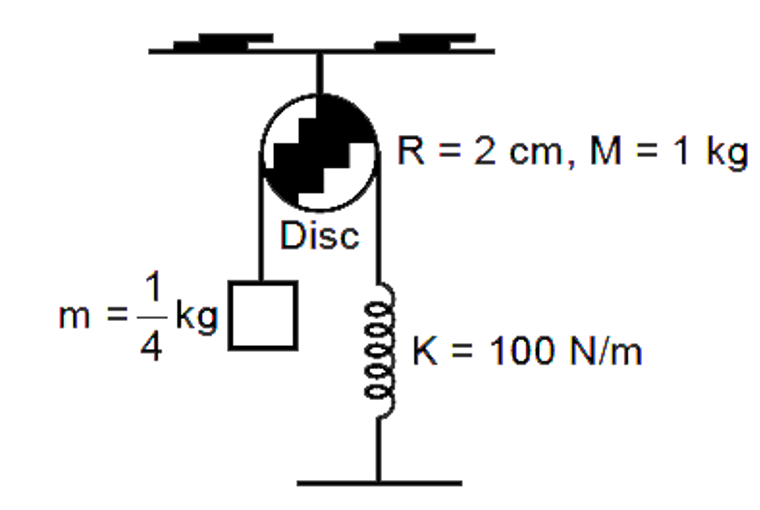
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration a=g2
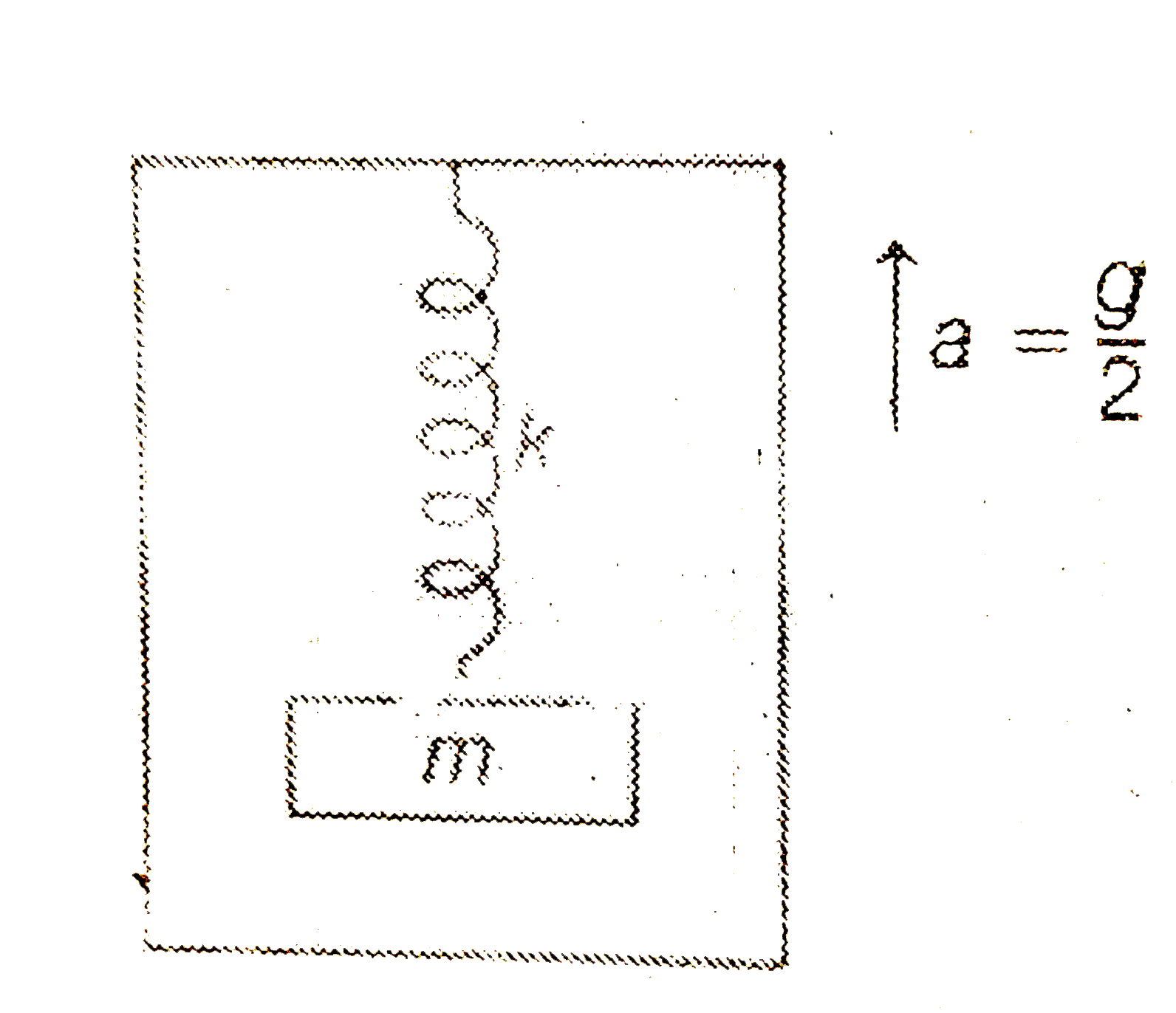
In mean position (of block's oscillations) spring is
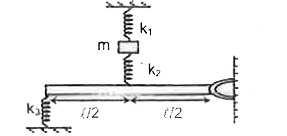
View SolutionFind the angular frequency of small oscillation of block m in the arrangement shown. Rod is massless. [Assume gravity to be absont]
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View Solution