The breaking stress of a wire depends on
length of wire
area of cross-section of wire
Both (a) and (b)
independent of length and area of cross-section
The correct Answer is:D
(d) Breaking stress is independent of length and area of cross-section.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.215videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.315videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective10videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
The breaking stress for a wire of radius r of given material is F N/m2. The breaking stress for the wire of same material of radius 2r is:
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
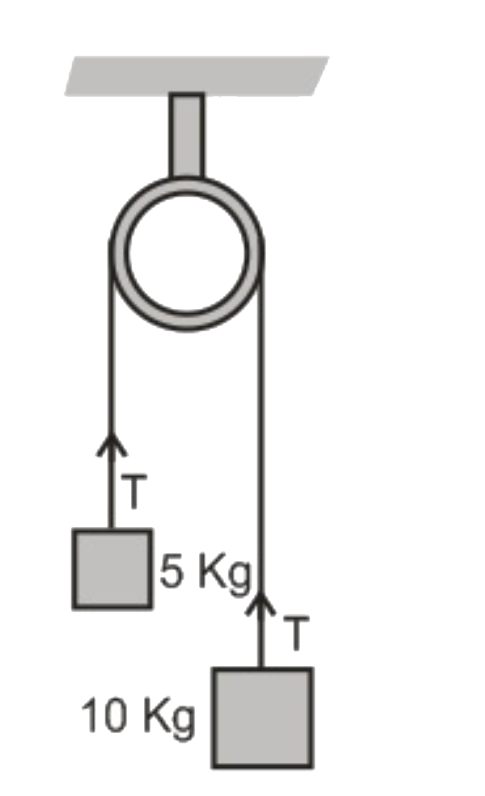 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The breaking stress for a wire of unit cross-section is called
Ayield pointBelastic fatigueCtensile strengthDYoung's modulus
Figure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area 10−6m2. The breaking stress of the wire is 7×106N/m2. The block is placed in a beaker of base area 200cm2 and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects 2cm3 of water per sec. Find the time at which the wire will break.
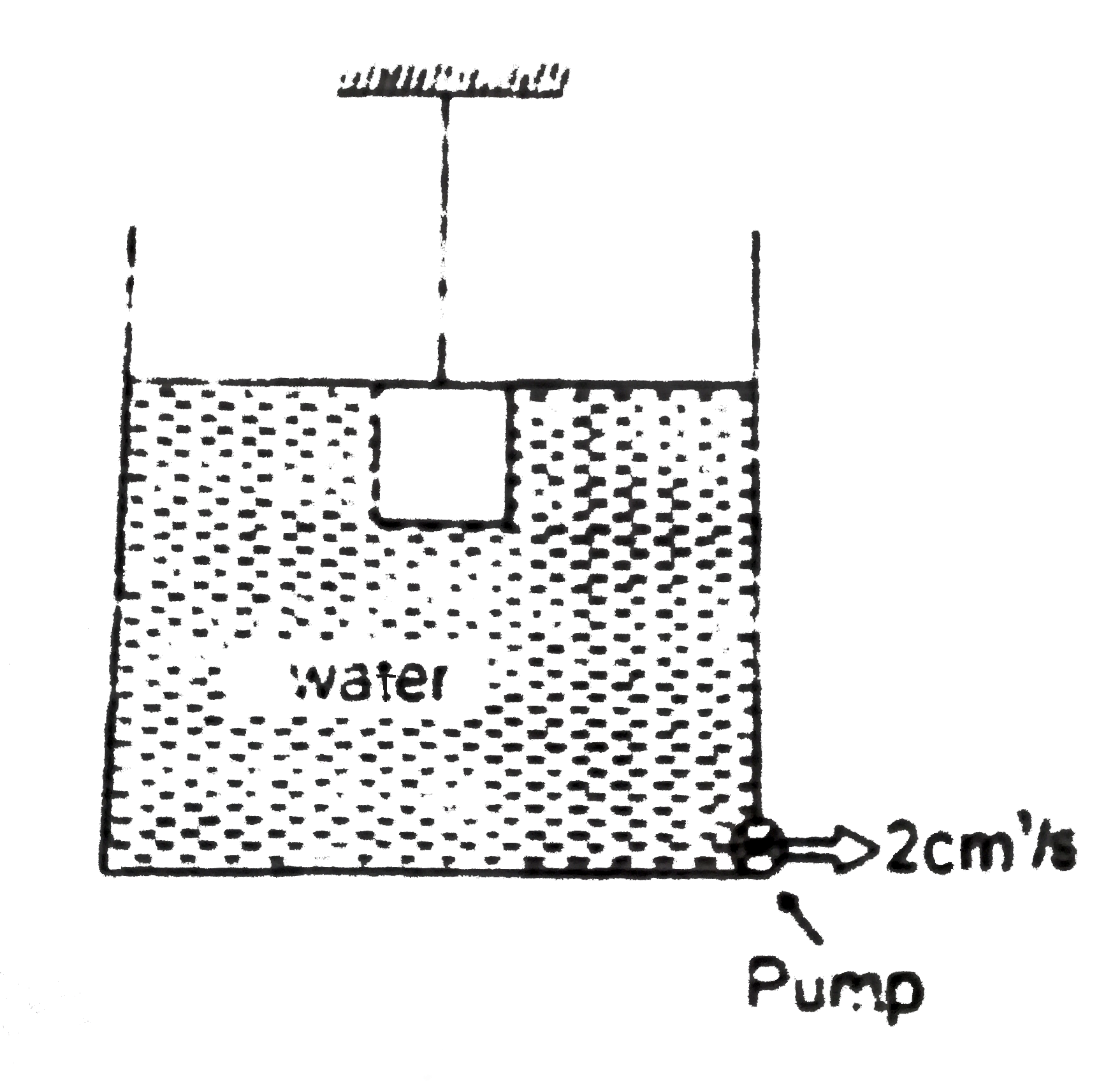 View Solution
View SolutionThe breaking stress of a material is 108Nm−2. Find the greatest length of a wire that could hang vertically without breaking? Density of material =3000kgm−3.
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
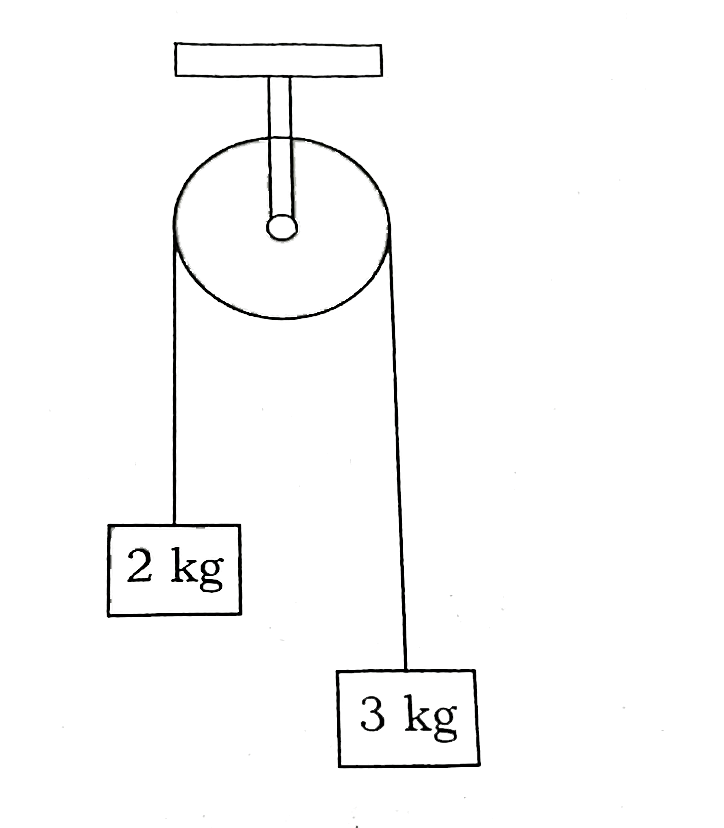 View Solution
View SolutionSpecific resistance of a wire depends on its
View SolutionSpecific resistance of a wire depends on its
View SolutionHow does the resistance of a wire depend on its radius? Explain your answer.
View SolutionThe breaking stress for a substance is 106N/m2. What length of the wire of this substance should be suspended verticaly so that the wire breaks under its own weight? (Given: density of material of the wire =4×103kg/m3 and g=10ms−12)
View Solution

