A short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
To solve the problem, we need to determine the orientations of the bar magnet that correspond to stable and unstable equilibrium in a uniform magnetic field, as well as calculate the potential energy in each case.
1. Understanding the Magnetic Moment and Magnetic Field:
- The magnetic moment (M) of the bar magnet is given as 0.32JT−1.
- The external magnetic field (B) is given as 0.15T.
2. Identifying Stable and Unstable Equilibrium:
- Stable Equilibrium: This occurs when the magnetic moment (M) is aligned parallel to the magnetic field (B). This means the angle θ between M and B is 0∘.
- Unstable Equilibrium: This occurs when the magnetic moment (M) is aligned anti-parallel to the magnetic field (B). This means the angle θ is 180∘.
3. Calculating Potential Energy:
- The potential energy (U) of a magnetic moment in a magnetic field is given by the formula:
U=−M⋅B⋅cos(θ)
4. Potential Energy in Stable Equilibrium:
- For stable equilibrium, θ=0∘:
Ustable=−M⋅B⋅cos(0∘)=−0.32⋅0.15⋅1
Ustable=−0.048J
5. Potential Energy in Unstable Equilibrium:
- For unstable equilibrium, θ=180∘:
Uunstable=−M⋅B⋅cos(180∘)=−0.32⋅0.15⋅(−1)
Uunstable=0.048J
Summary of Results:
- Stable Equilibrium Orientation: Magnetic moment parallel to the magnetic field (θ=0∘).
- Unstable Equilibrium Orientation: Magnetic moment anti-parallel to the magnetic field (θ=180∘).
- Potential Energy in Stable Equilibrium: −0.048J.
- Potential Energy in Unstable Equilibrium: 0.048J.
- The magnetic moment (M) of the bar magnet is given as 0.32JT−1.
- The external magnetic field (B) is given as 0.15T.
- Stable Equilibrium: This occurs when the magnetic moment (M) is aligned parallel to the magnetic field (B). This means the angle θ between M and B is 0∘.
- Unstable Equilibrium: This occurs when the magnetic moment (M) is aligned anti-parallel to the magnetic field (B). This means the angle θ is 180∘.
- The potential energy (U) of a magnetic moment in a magnetic field is given by the formula:
U=−M⋅B⋅cos(θ)
- For stable equilibrium, θ=0∘:
Ustable=−M⋅B⋅cos(0∘)=−0.32⋅0.15⋅1
Ustable=−0.048J
- For unstable equilibrium, θ=180∘:
Uunstable=−M⋅B⋅cos(180∘)=−0.32⋅0.15⋅(−1)
Uunstable=0.048J
- Stable Equilibrium Orientation: Magnetic moment parallel to the magnetic field (θ=0∘).
- Unstable Equilibrium Orientation: Magnetic moment anti-parallel to the magnetic field (θ=180∘).
- Potential Energy in Stable Equilibrium: −0.048J.
- Potential Energy in Unstable Equilibrium: 0.048J.
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.1
15 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - 5.2
15 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A short bar magnet of magnetic moment 0⋅4JT−1 is placed in a uniform magnetic field of 0⋅16T. The magnet is in stable equilibrium when the potencial energy is
View SolutionA short bar magnet having magnetic moment M=0.80JT1 is placed in uniform magnetic field of 0.30 T. If bar magnet is free to rotate in plane of field, then (where U is potential energy and tau is torque)
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

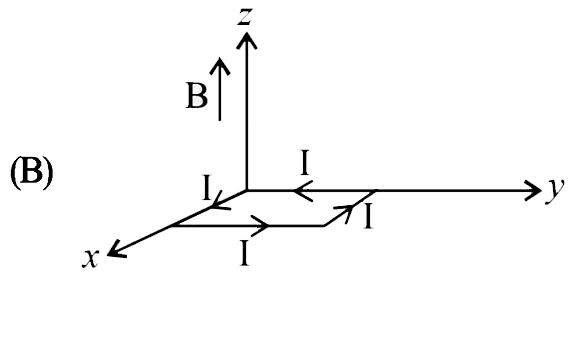

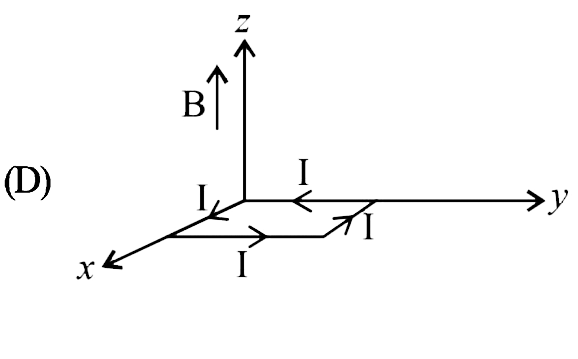
View SolutionA magnet of magnetic moment 2JT−1 is aligned in the direction of magnetic field of 0.1T. What is the net work done to bring the magnet normal to the magnrtic field?
View SolutionThe potential enargy of bar magnet of magnetic moment 8Am2 placed in a uniform magnetic field of 2 T at an angle of 120∘ is equal to
View SolutionA short bar magnetic is placed in a uniform magnetic field of 0.25 T, with its axis at an angle of 30∘ with the field. If it experiences a torque of magnitude 4.5×10−2 N m, then its magnetic momentum is
View SolutionA bar magnet of magnetic moment 6 J/T is aligned at 60∘ with a uniform external magnetic field of 0.44 T. Calculate (a) the work done in turning the magnet to align its magnetic moment (i) normal to the magnetic field, (ii) opposite to the magnetic field, and (b) the torque on the magnet in the final orientation in case (ii).
View SolutionA bar magnet of magnetic moment 3.0A−m2 is placed in a uniform magnetic induction field of 2×10−5T. If each pole of the magnet experiences a force of 6×10−4N, the length of the magnet is
View SolutionA short bar magnet pleaced with its axis at 30∘ with a uniform external magnetic field of 0.16 Tesla expriences a torque of magnitude 0.032 Joule. The magnetic moment of the bar magnet will be
View SolutionShort bar magnet is place 30degrees with the external magnetic field 0.06T which experiences a torque of 0.018Nm then the minimum work done required to move from its stable equilibrium to unstable equilibrium is
View Solution
