Short bar magnet is place 30degrees with the external magnetic field 0.06T which experiences a torque of 0.018Nm then the minimum work done required to move from its stable equilibrium to unstable equilibrium is
9.2×10−3J
7.2×10−2J
6.4×10−2J
11.7×10−3J
The correct Answer is:B
To solve the problem step by step, we will follow the concepts of torque and work done on a magnetic dipole in an external magnetic field.
Step 1: Understand the Equilibrium Positions
- The stable equilibrium position of the magnet is when it is aligned with the magnetic field, which corresponds to an angle θ=0∘.
- The unstable equilibrium position is when the magnet is anti-aligned with the magnetic field, which corresponds to an angle θ=180∘.
Step 2: Torque on the Magnet
The torque τ experienced by a magnetic dipole in a magnetic field is given by the formula:
τ=mBsinθ
where:
- m is the magnetic moment,
- B is the magnetic field strength,
- θ is the angle between the magnetic moment and the magnetic field.
Step 3: Calculate the Magnetic Moment
Given that the torque τ=0.018Nm, the magnetic field B=0.06T, and the angle θ=30∘, we can rearrange the torque formula to find the magnetic moment m:
m=τBsinθ
Substituting the known values:
m=0.0180.06⋅sin(30∘)
Since sin(30∘)=0.5:
m=0.0180.06⋅0.5=0.0180.03=0.6A m2
Step 4: Calculate the Work Done
The work done W to move the magnet from stable equilibrium to unstable equilibrium is given by:
W=Uunstable−Ustable
Where the potential energy U of a magnetic dipole in a magnetic field is given by:
U=−mBcosθ
- At stable equilibrium (θ=0∘):
Ustable=−mBcos(0)=−mB
- At unstable equilibrium (θ=180∘):
Uunstable=−mBcos(180)=mB
Thus, the work done is:
W=(mB)−(−mB)=2mB
Substituting the values:
W=2⋅0.6⋅0.06=0.072J=7.2×10−2J
Final Answer
The minimum work done required to move the magnet from stable equilibrium to unstable equilibrium is:
7.2×10−2J
- The stable equilibrium position of the magnet is when it is aligned with the magnetic field, which corresponds to an angle θ=0∘.
- The unstable equilibrium position is when the magnet is anti-aligned with the magnetic field, which corresponds to an angle θ=180∘.
The torque τ experienced by a magnetic dipole in a magnetic field is given by the formula:
τ=mBsinθ
where:
- m is the magnetic moment,
- B is the magnetic field strength,
- θ is the angle between the magnetic moment and the magnetic field.
Given that the torque τ=0.018Nm, the magnetic field B=0.06T, and the angle θ=30∘, we can rearrange the torque formula to find the magnetic moment m:
m=τBsinθ
Substituting the known values:
m=0.0180.06⋅sin(30∘)
Since sin(30∘)=0.5:
m=0.0180.06⋅0.5=0.0180.03=0.6A m2
The work done W to move the magnet from stable equilibrium to unstable equilibrium is given by:
W=Uunstable−Ustable
Where the potential energy U of a magnetic dipole in a magnetic field is given by:
U=−mBcosθ
- At stable equilibrium (θ=0∘):
Ustable=−mBcos(0)=−mB
- At unstable equilibrium (θ=180∘):
Uunstable=−mBcos(180)=mB
Thus, the work done is:
W=(mB)−(−mB)=2mB
Substituting the values:
W=2⋅0.6⋅0.06=0.072J=7.2×10−2J
The minimum work done required to move the magnet from stable equilibrium to unstable equilibrium is:
7.2×10−2J
Topper's Solved these Questions
Similar Questions
A short bar magnet placed with its axis at 30∘ with an external field of 800 G experiences a torque of 0.016 Nm.
What is the magnetic moment of the magnet ?
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

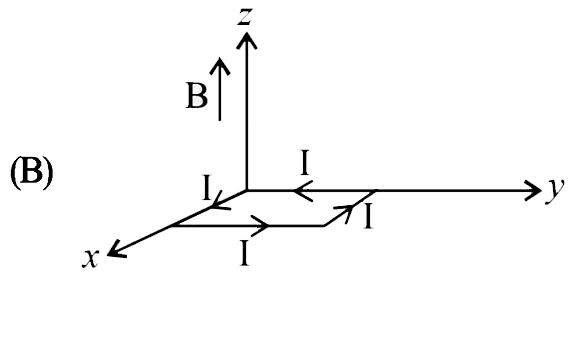

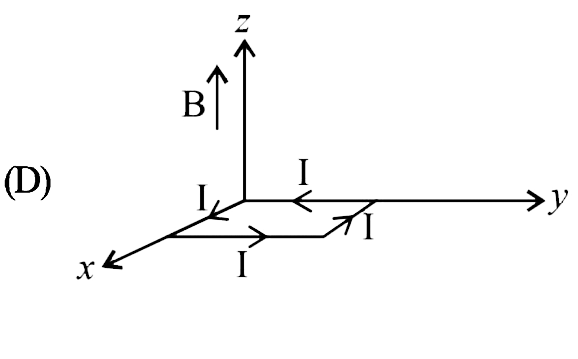
View Solution
Knowledge Check
A short bar magnet placed with its axis at 30∘ with a uniform external magnetic field of 0.35 T experiences a torque of magnitude equal to 4.5×10−2Nm. The magnitude of magnetic moment of the given magnet is
A0.26JT−1B2.6JT−1C0.26JT−1D0.026JT−1A rectangular loop of sides 10cm and 5cm carrying a current I of 12A is placed in different orienctations as shown in the figure
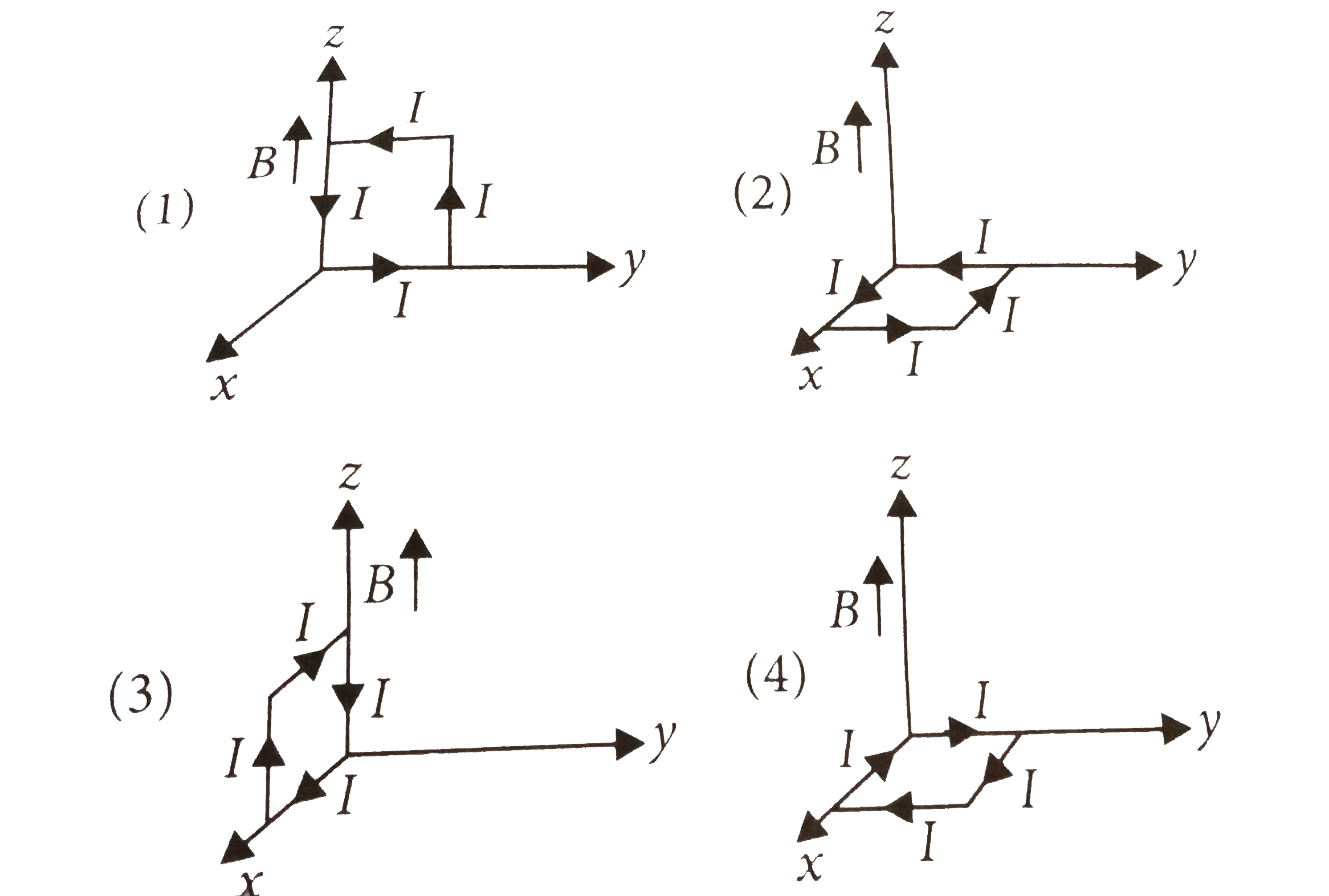
If there is a uniform magnetic field of 0.3 T in the positive z-direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium .A(2)and(4), respectivelyB(2)and(3), respectivelyC(1)and(2), respectivelyD(1)and(3), respectivelyThe magnetic moment of a short bar magnet placed with its magnetic axis at 30∘ to an external field of 900 G and experiences a torque of 0.02 N m is
A0.35Am2B0.44Am2C2.45Am2D1.5Am2
A short bar magnet pleaced with its axis at 30∘ with a uniform external magnetic field of 0.16 Tesla expriences a torque of magnitude 0.032 Joule. The magnetic moment of the bar magnet will be
View SolutionA short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View SolutionA short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View SolutionA short bar magnet placed with its axis at 30∘ with a uniform external magnetic field of 0⋅25T experiences a torque of magnitude equal to 4⋅5×10−2J. What is the magnitude of magnetic moment of the magnet?
View SolutionA short bar magnetic is placed in a uniform magnetic field of 0.25 T, with its axis at an angle of 30∘ with the field. If it experiences a torque of magnitude 4.5×10−2 N m, then its magnetic momentum is
View Solution
