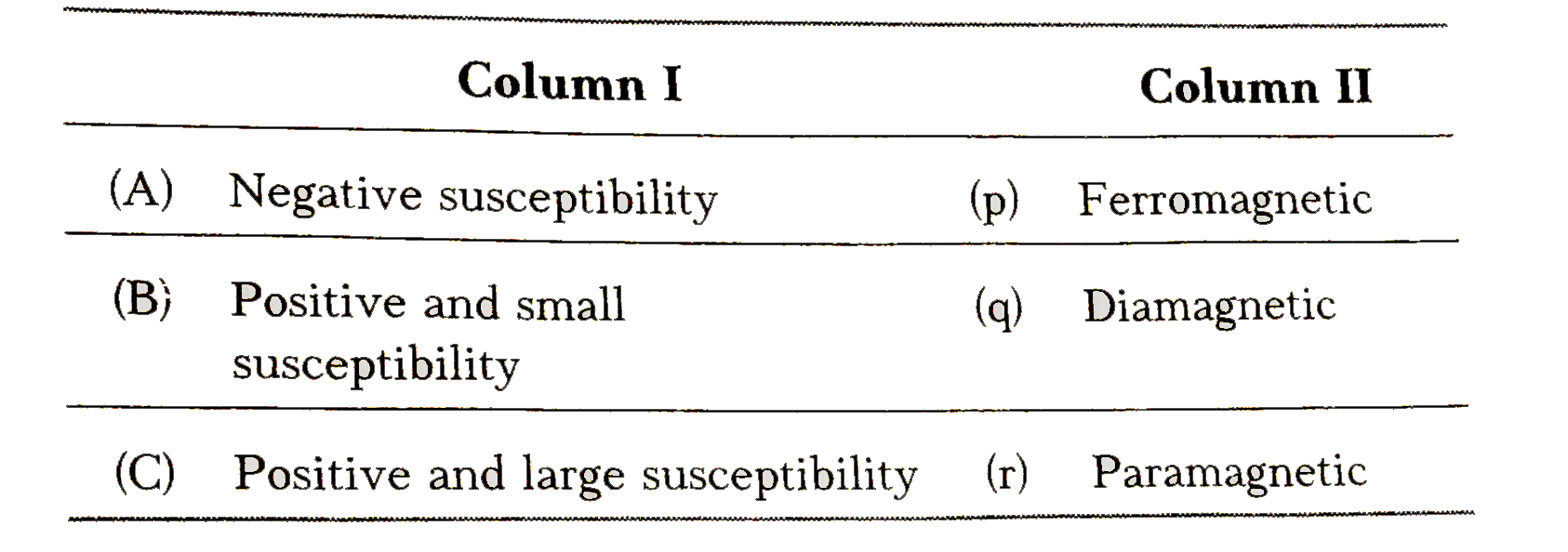Consider the expression for magnetic potential energy Um obtained in previous question, match the tems of colum I with the tems of Column II and choose the correct option from the codes given below.
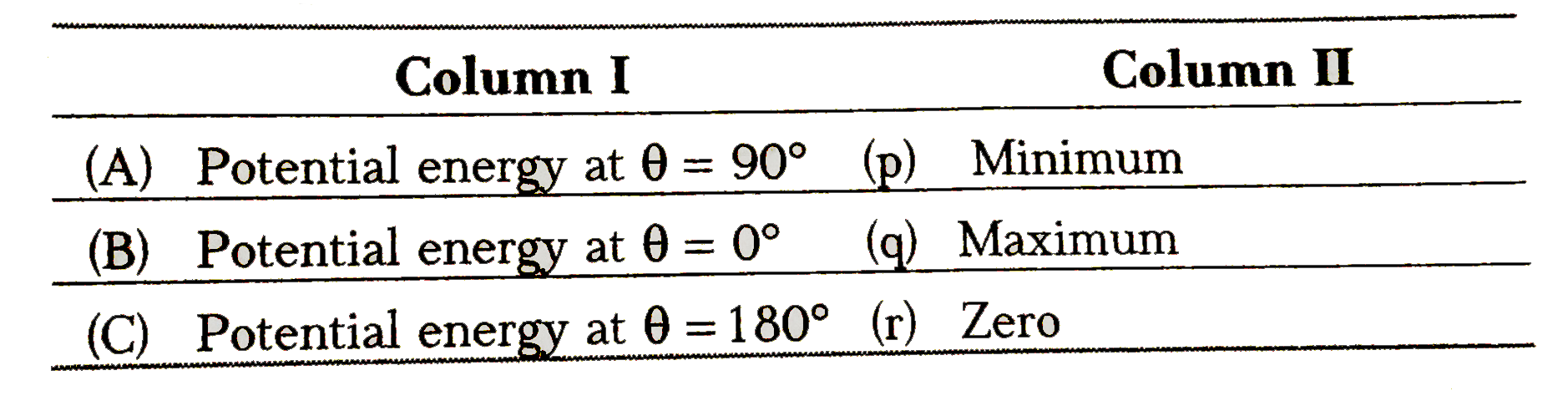
Video Solution
Text Solution
The correct Answer is:A-R,B-P,C-Q
Since the magnetic potential energy Um is given by.
Um=m.B=−mBcosθ
A Forθ=90∘⇒Um=−mBcos90∘=0
B Forθ=0∘,Um=−mBcos0∘=−mB
The potential energy is minimum and hence the middle the needle is in most stable position.
C Forθ=180∘,Um=−mBcos180∘=+mB
|
Similar Questions
Knowledge Check
Match the two columns and select the correct option from the codes given below.
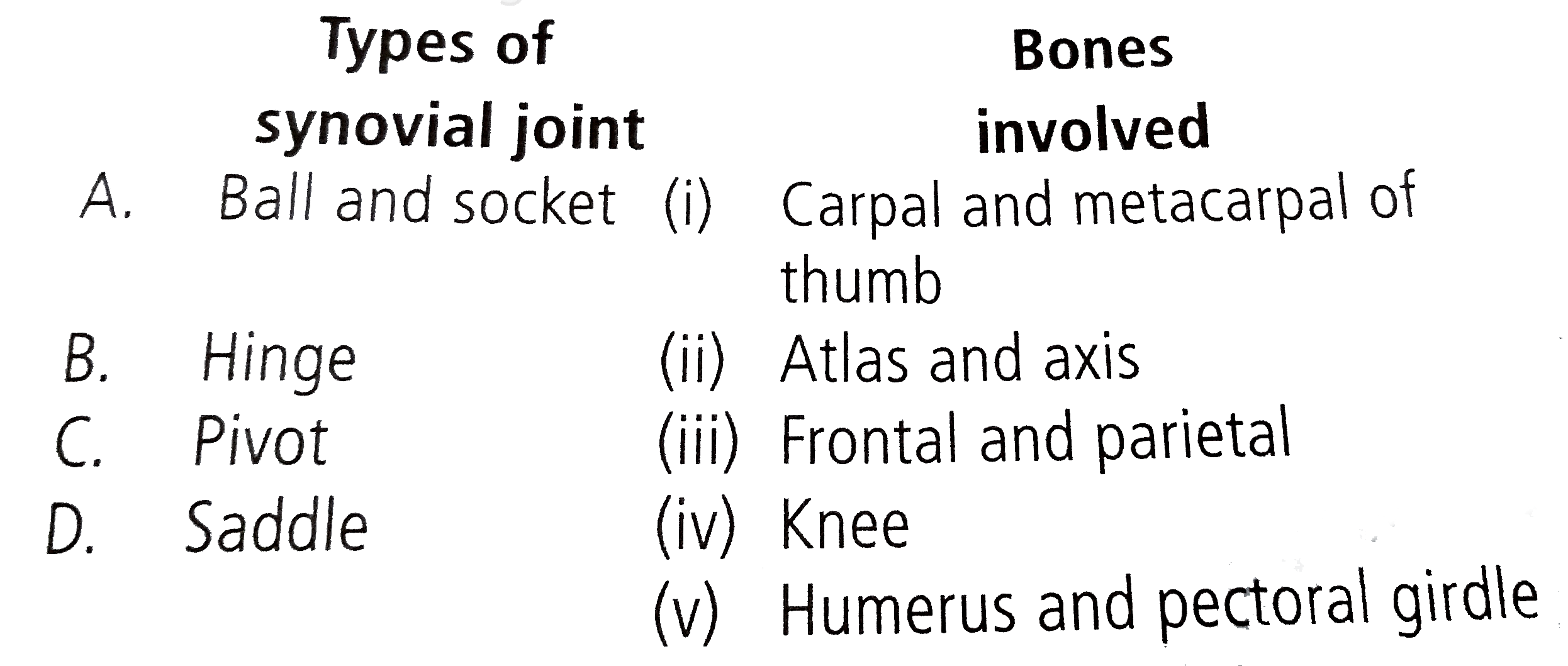 AA-(v),B-(iv),C-(ii),D-(i)BA-(i),B-(iii),C-(iv),D-(v)CA-(v),B-(iv),C-(iii),D-(i)DA-(i),B-(ii),C-(v),D-(iv)
AA-(v),B-(iv),C-(ii),D-(i)BA-(i),B-(iii),C-(iv),D-(v)CA-(v),B-(iv),C-(iii),D-(i)DA-(i),B-(ii),C-(v),D-(iv)
Match the items of column I with those of Column II and choose the correct option from the codes given below.

View SolutionMatch the Column I with Column II and choose the correct option from the codes given below.

View SolutionWith reference to magnetic dipole, match the tems of Column I with the tems of Column Ii and Choose the correct option from the codes given below.

View SolutionMatch the List with List II and choose the correct option from the codes given below:

View SolutionMatch the entities of column I with column II and choose the right option from the codes given below

View SolutionMatch Column - I with Column -II and select the correct option from the codes given below .

View SolutionMatch Column I with Column II and select correct option from the codes given below.

View Solution