Consider the following statements: (a)An emf can be induced by moving a conductor in a magnetic field. (b)An emf can be induced by changing the magnetic field.
Both A and B are true
A is true but B is false
B is true but A is false
Both A and B are false
The correct Answer is:A
To analyze the given statements regarding electromagnetic induction, we will evaluate each statement step by step.
Step 1: Evaluate Statement (a)
Statement (a): An emf can be induced by moving a conductor in a magnetic field.
1. Understanding the Concept: According to the principle of electromagnetic induction, when a conductor moves through a magnetic field, an electromotive force (emf) is induced across the ends of the conductor. This is known as motional emf.
2. Mathematical Representation: The induced emf (ε) can be calculated using the formula:
ϵ=B⋅L⋅v
where:
- B is the magnetic field strength,
- L is the length of the conductor,
- v is the velocity of the conductor relative to the magnetic field.
3. Conclusion: Since the statement mentions that an emf "can be induced," it is true. There are conditions under which this occurs, specifically when the conductor is moving perpendicularly to the magnetic field lines.
Step 2: Evaluate Statement (b)
Statement (b): An emf can be induced by changing the magnetic field.
1. Understanding the Concept: According to Faraday's law of electromagnetic induction, a change in magnetic flux through a closed loop induces an emf in that loop. This can occur even if the conductor is stationary, as long as the magnetic field is changing.
2. Mathematical Representation: The induced emf (ε) due to a change in magnetic flux (Φ) is given by:
ϵ=−dΦdt
where:
- Φ is the magnetic flux, defined as B⋅A (B is the magnetic field and A is the area through which the field lines pass).
3. Conclusion: Since the statement indicates that an emf "can be induced" by changing the magnetic field, it is also true. The change in the magnetic field leads to a change in magnetic flux, which induces an emf.
Final Conclusion
Both statements (a) and (b) are true. Therefore, we conclude that:
- Statement (a) is true: An emf can be induced by moving a conductor in a magnetic field.
- Statement (b) is true: An emf can be induced by changing the magnetic field.
Summary
Both statements are true as they align with the principles of electromagnetic induction.
---
Statement (a): An emf can be induced by moving a conductor in a magnetic field.
2. Mathematical Representation: The induced emf (ε) can be calculated using the formula:
ϵ=B⋅L⋅v
where:
- B is the magnetic field strength,
- L is the length of the conductor,
- v is the velocity of the conductor relative to the magnetic field.
Statement (b): An emf can be induced by changing the magnetic field.
ϵ=−dΦdt
where:
- Φ is the magnetic flux, defined as B⋅A (B is the magnetic field and A is the area through which the field lines pass).
Both statements (a) and (b) are true. Therefore, we conclude that:
- Statement (b) is true: An emf can be induced by changing the magnetic field.
Both statements are true as they align with the principles of electromagnetic induction.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
What rule do we use to find the direction of induced current in a conductor moving in a magnetic field?
AFleming's left hand ruleBFleming's right hand ruleCAmpere's ruleDRight hand clasp rule
A metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
View SolutionA metallic loop is placed in a non-uniform steady magnetic field. Will an emf be induced in the loop?
View SolutionA coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
View SolutionA coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
View SolutionThe total charge induced in a conducting loop when it is moved in magnetic field depends on
View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)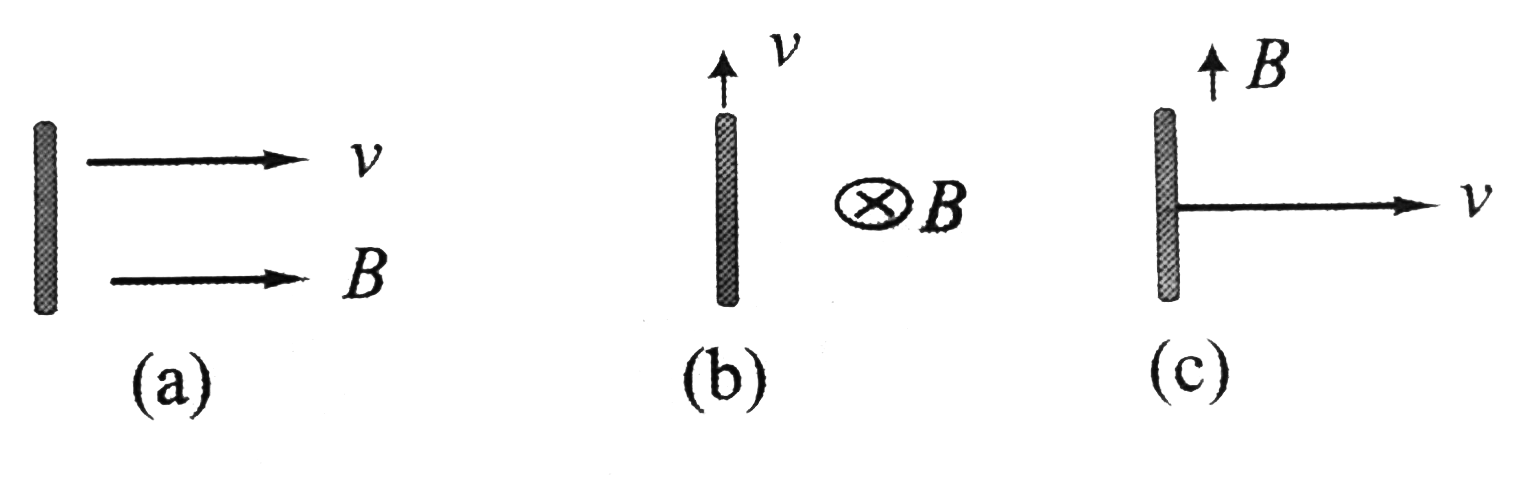
View SolutionA circular loop of radius 1m is placed in a varying magnetic field given as B=6t Tesla, where t is time in sec.
(a)Find the emf induced in the coil if the plane of the coil is perpendicular to the magnetic field.
(b) Find the electric field in the tangential directin, induced due to the changing magnetic field.
(c)Find the current in the loop if its resistance is 1Ω/m.
View Solution