Assertion An induced emf of 2 V is developed in a circular loop, if current in the loop is changed at a rate of 4 As−1 .IF 4 A of current is passed through this loop, then flux linked with this coil will be 2 Wb.
Reason Flux linked with the coil is
|ϕ|=∣∣∣edi/dt∣∣∣i
If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:A
To solve the given problem, we will analyze both the assertion and the reason step by step.
Step 1: Understanding the Given Information
We are provided with:
- An induced emf (E) of 2 V.
- A rate of change of current (di/dt) of 4 A/s.
- A current (I) of 4 A flowing through the loop.
Step 2: Using the Formula for Induced EMF
The induced emf in a coil can be expressed using the formula:
E=Ldidt
where L is the inductance of the coil.
Step 3: Rearranging the Formula to Find Inductance
From the formula above, we can rearrange it to find the inductance L:
L=Edidt
Substituting the known values:
L=2V4A/s=0.5H
Step 4: Finding the Magnetic Flux Linked with the Coil
The magnetic flux Φ linked with the coil can be expressed as:
Φ=L⋅I
Substituting the values we have:
Φ=0.5H⋅4A=2Wb
Step 5: Conclusion
The assertion states that the flux linked with the coil will be 2 Wb, which we have calculated to be true. Therefore, the assertion is correct.
Step 6: Validating the Reason
The reason provided states that:
|Φ|=∣∣
∣∣Edidt∣∣
∣∣I
This is consistent with our calculations since we derived that:
Φ=L⋅I
and L was calculated as Edidt. Thus, the reason is also correct.
Final Answer
Both the assertion and the reason are true, and the reason correctly explains the assertion.
---
We are provided with:
- An induced emf (E) of 2 V.
- A rate of change of current (di/dt) of 4 A/s.
- A current (I) of 4 A flowing through the loop.
The induced emf in a coil can be expressed using the formula:
E=Ldidt
where L is the inductance of the coil.
From the formula above, we can rearrange it to find the inductance L:
L=Edidt
Substituting the known values:
L=2V4A/s=0.5H
The magnetic flux Φ linked with the coil can be expressed as:
Φ=L⋅I
Substituting the values we have:
Φ=0.5H⋅4A=2Wb
The assertion states that the flux linked with the coil will be 2 Wb, which we have calculated to be true. Therefore, the assertion is correct.
The reason provided states that:
|Φ|=∣∣
∣∣Edidt∣∣
∣∣I
This is consistent with our calculations since we derived that:
Φ=L⋅I
and L was calculated as Edidt. Thus, the reason is also correct.
Both the assertion and the reason are true, and the reason correctly explains the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together119videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Two coils X and Y are linked such that emf E is induced in Y when the current in x is changing at the rate I'(=dI/dt). If a current I0 is now made to flow through Y, the flux linked with X will be
View SolutionThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
View SolutionAssertion If current passing through a circular loop is doubled, then magnetic flux linked with the circular loop will also become two times.
Reason No flux will link through the coil by its own current.View SolutionFigure shows two concentric loops of radii R and r (R gtgt r). A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View SolutionCurrent (i) passing through a coil varies with time t as i=2t2. At 1 s total flux passing through the coil is 10 Wb. Then
View SolutionA rectangular loop of area 0.06 m2 is placed in a magnetic field of 0.3T with its plane inclined 30∘ to the field. Find the flux linked with the coil .
View SolutionThe mutual inductance between two coils is 2.5H. If the current in one coil is changed at the rate of 1As−1, what will be the emf induced in the other coil?
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
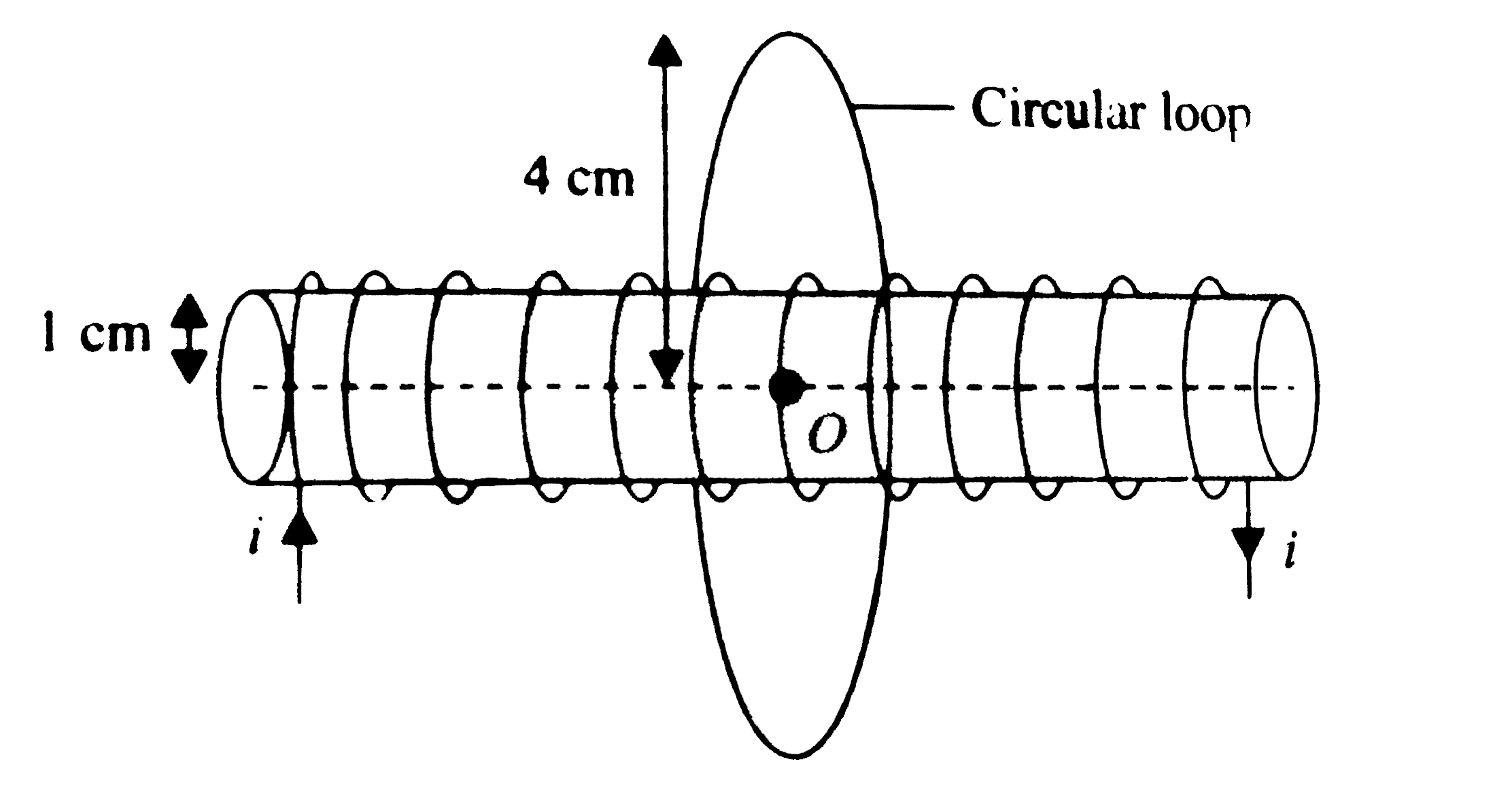
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView SolutionWhenever the magnet flux linked with a coil changes, then is an induced emf in the circuit. This emf lasts
View SolutionAn emf of 25.0 mV is induced in a 500-turn coil when the current is changing is at the rate of 10.0A/s. What is the magnetic flux through each turn of the coil at an instant when the current is 4.0A?
View Solution

