A circuits contains a capacitor and inductance each with negligible resistance. The capacitor is initially charged and the charging battery is disconnected. At subsequent time , the charge on the capacitor will
increase exponentially
decrease exponentially
decrease linearly
remain constant
The correct Answer is:C
To solve the problem of how the charge on the capacitor varies over time in a circuit containing a capacitor and an inductor with negligible resistance, we can follow these steps:
1. Understanding the Circuit:
- We have a capacitor (C) that is initially charged and an inductor (L) connected in parallel. The battery is disconnected, meaning no external voltage is applied.
2. Energy Conservation:
- The energy stored in the capacitor is given by UC=12CV2 or UC=12Q2C, where Q is the charge on the capacitor.
- The energy stored in the inductor is given by UL=12LI2, where I is the current through the inductor.
3. Energy Transfer:
- When the battery is disconnected, the energy will oscillate between the capacitor and the inductor. The total energy in the system remains constant, so:
12CV2+12LI2=constant
4. Using Kirchhoff's Law:
- The relationship between the charge Q on the capacitor and the current I through the inductor can be expressed as:
I=dQdt
- Thus, we can write the equation for the inductor:
LdIdt=QC
5. Differential Equation:
- Substituting I=dQdt into the inductor equation gives:
Ld2Qdt2=−QC
- Rearranging this yields:
d2Qdt2+1LCQ=0
- This is a second-order linear differential equation, which is characteristic of simple harmonic motion (SHM).
6. Solution of the Differential Equation:
- The general solution for this equation is:
Q(t)=Q0cos(ωt+ϕ)
- where ω=1√LC, Q0 is the maximum charge, and ϕ is the phase constant.
7. Conclusion:
- The charge Q(t) on the capacitor oscillates sinusoidally over time with a fixed amplitude Q0. Therefore, the charge does not decrease or increase; it simply oscillates between maximum and minimum values.
Final Answer:
The charge on the capacitor will oscillate and remain constant in total energy, as there is no loss of charge due to negligible resistance.
- We have a capacitor (C) that is initially charged and an inductor (L) connected in parallel. The battery is disconnected, meaning no external voltage is applied.
- The energy stored in the capacitor is given by UC=12CV2 or UC=12Q2C, where Q is the charge on the capacitor.
- The energy stored in the inductor is given by UL=12LI2, where I is the current through the inductor.
- When the battery is disconnected, the energy will oscillate between the capacitor and the inductor. The total energy in the system remains constant, so:
12CV2+12LI2=constant
- The relationship between the charge Q on the capacitor and the current I through the inductor can be expressed as:
I=dQdt
- Thus, we can write the equation for the inductor:
LdIdt=QC
- Substituting I=dQdt into the inductor equation gives:
Ld2Qdt2=−QC
- Rearranging this yields:
d2Qdt2+1LCQ=0
- This is a second-order linear differential equation, which is characteristic of simple harmonic motion (SHM).
- The general solution for this equation is:
Q(t)=Q0cos(ωt+ϕ)
- where ω=1√LC, Q0 is the maximum charge, and ϕ is the phase constant.
- The charge Q(t) on the capacitor oscillates sinusoidally over time with a fixed amplitude Q0. Therefore, the charge does not decrease or increase; it simply oscillates between maximum and minimum values.
The charge on the capacitor will oscillate and remain constant in total energy, as there is no loss of charge due to negligible resistance.
Similar Questions
A parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
View SolutionIn the given circuit, the charge on 4μF capacitor will be :

View SolutionIn the given circuit, the charge on 4μF capacitor will be :
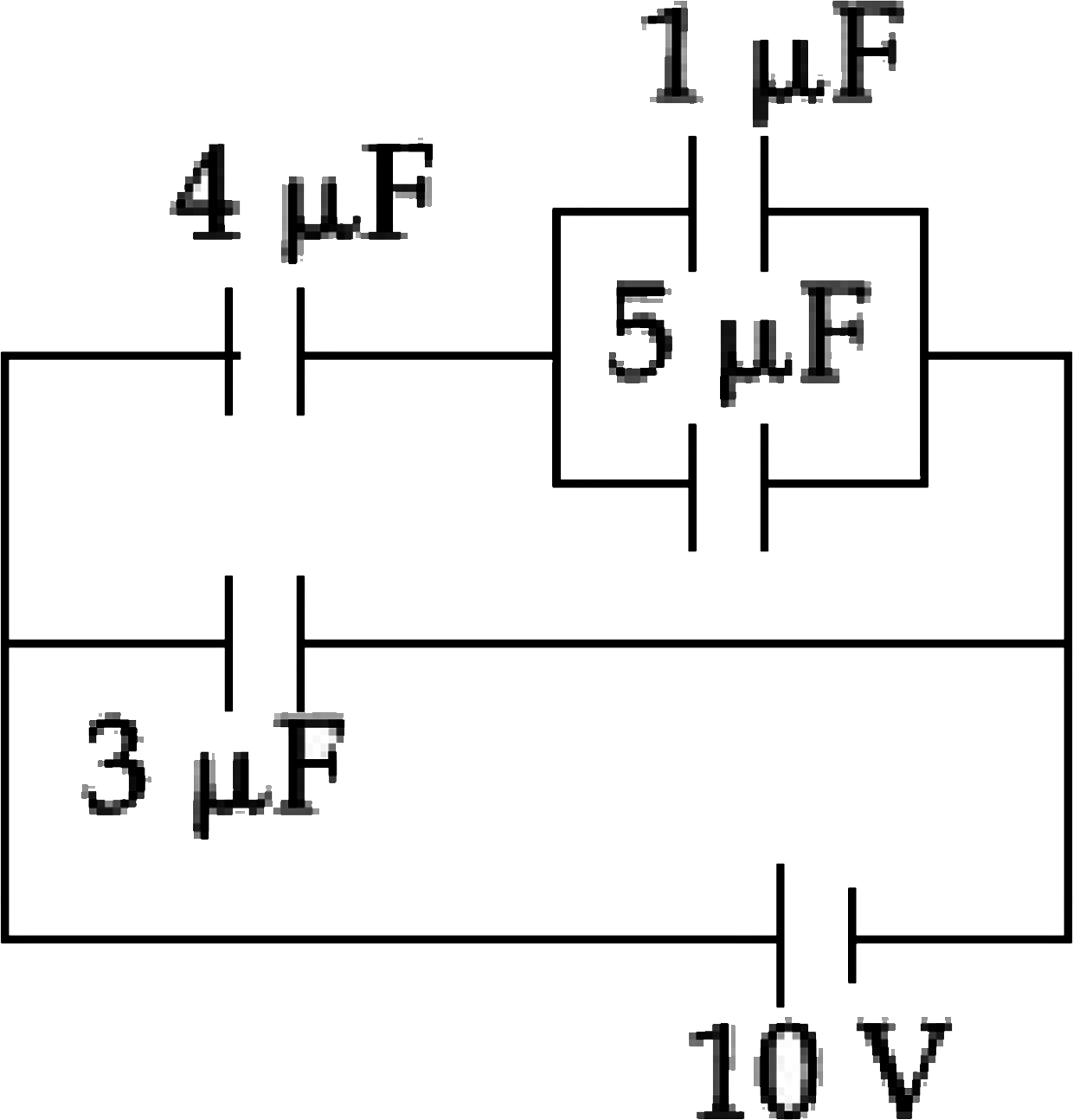 .
.
View SolutionIn the circuit shown below, the charge on the 60μF capacitor is

View SolutionThree initially uncharged capacitors are arranged with batteries as shown in. Find the charge on each capacitor.
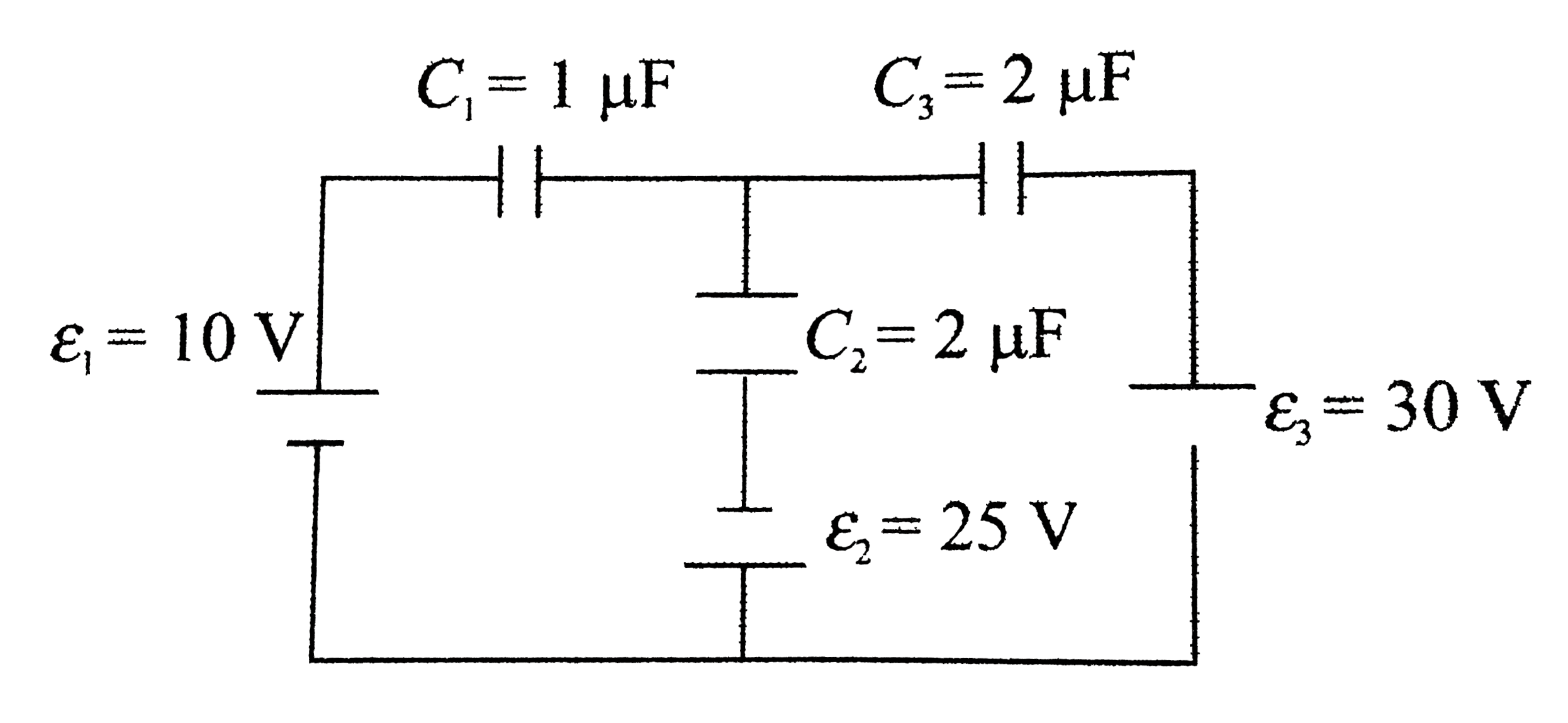 .
.
View SolutionIf the capacitor shown in the circuit is charged to 5V and left in the circuit, in 12s the charge on the capacitor will become:
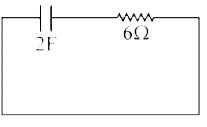
View SolutionA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
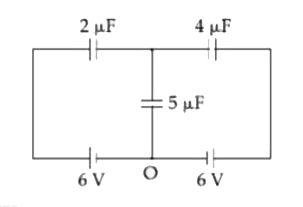
View SolutionThe circuit is in a steady state.
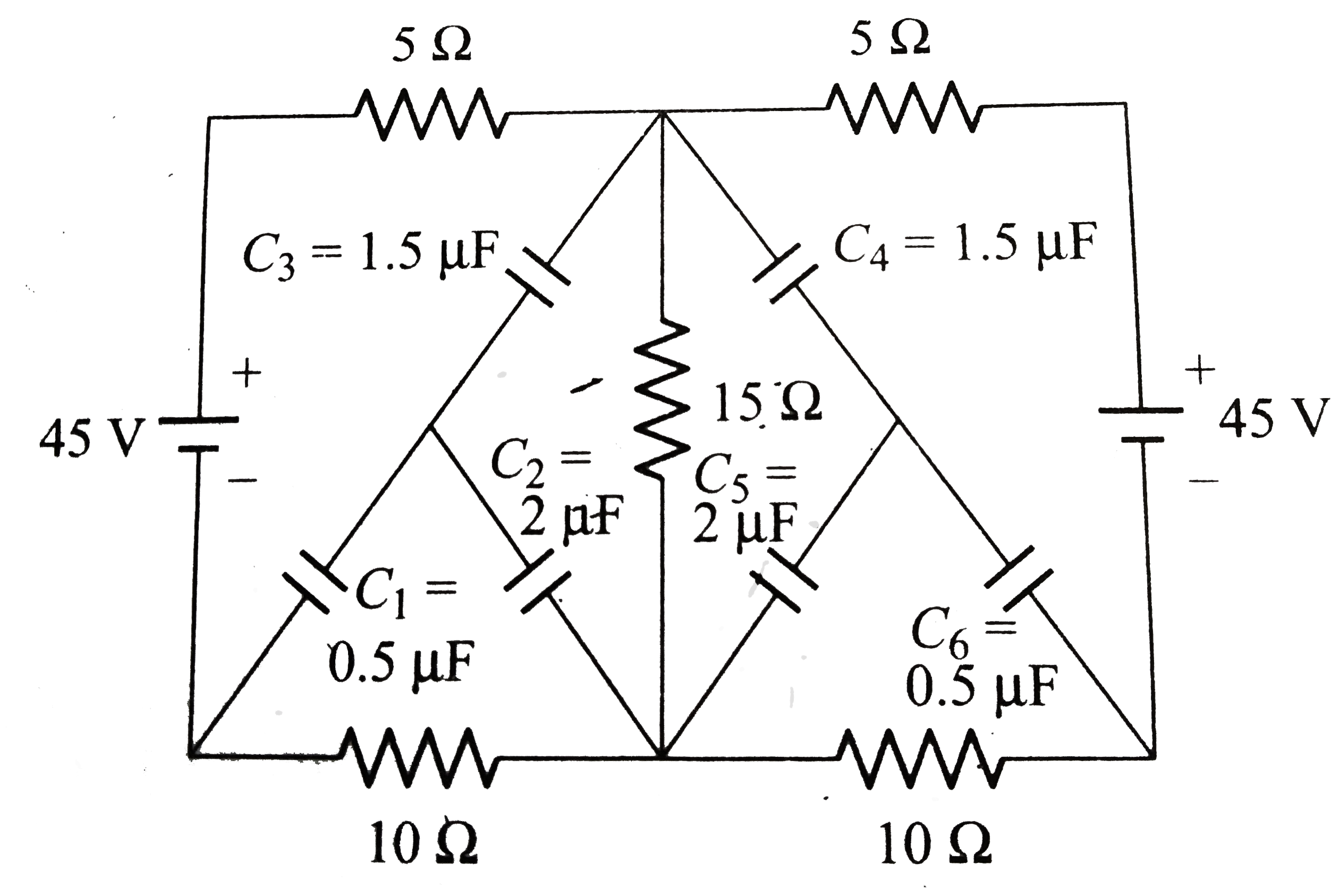
The charge in capacitor C3 is
View SolutionThe circuit is in a steady state.
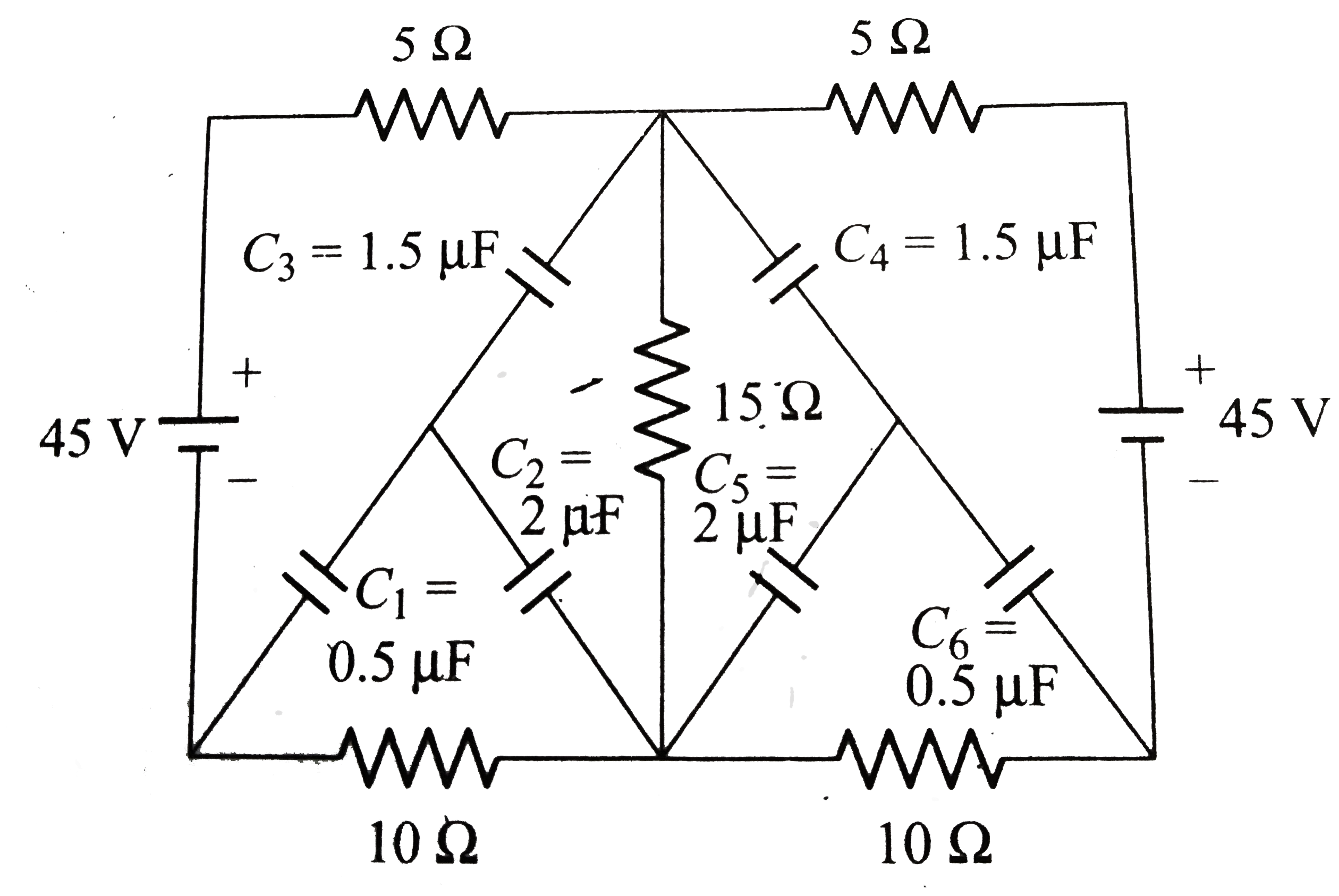
The charge in capacitor C1 is
View Solution
