Assertion: If an inductor coil is connected to DC source, the current supplied by it is I1. If the same coil is connected with an AC source of same voltage. Then current is I2, then I2<I1.
Reason: In AC circuit, inductor coil offers more resistance.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
To solve the given problem, we need to analyze the assertion and reason provided in the question step by step.
Step 1: Understand the Assertion
The assertion states that when an inductor coil is connected to a DC source, the current supplied is I1. When the same coil is connected to an AC source of the same voltage, the current is I2, and it claims that I2<I1.
Step 2: Analyze the Behavior of the Inductor in DC
When an inductor is connected to a DC source, it behaves like a short circuit after a transient period. The current through the inductor can be calculated using Ohm's law:
I1=VR
where V is the voltage of the DC source and R is the resistance of the circuit.
Step 3: Analyze the Behavior of the Inductor in AC
When the same inductor is connected to an AC source, the inductor introduces inductive reactance (XL), which affects the total impedance (Z) of the circuit. The impedance in an AC circuit with an inductor is given by:
Z=√R2+X2L
The current in the AC circuit can be calculated as:
I2=VZ
Step 4: Compare the Currents
Since Z (impedance) is always greater than R (resistance) in an AC circuit with an inductor, we can conclude:
I2=VZ<VR=I1
Thus, I2<I1 is indeed correct.
Step 5: Understand the Reason
The reason states that in an AC circuit, the inductor coil offers more resistance. This is true because the inductive reactance XL contributes to the total impedance Z, making it larger than just the resistance R. Therefore, the current I2 is reduced due to the increased total impedance.
Conclusion
Both the assertion and the reason are correct, and the reason correctly explains the assertion.
Final Answer
Both assertion and reason are correct, and the reason is the correct explanation for the assertion.
---
The assertion states that when an inductor coil is connected to a DC source, the current supplied is I1. When the same coil is connected to an AC source of the same voltage, the current is I2, and it claims that I2<I1.
When an inductor is connected to a DC source, it behaves like a short circuit after a transient period. The current through the inductor can be calculated using Ohm's law:
I1=VR
where V is the voltage of the DC source and R is the resistance of the circuit.
When the same inductor is connected to an AC source, the inductor introduces inductive reactance (XL), which affects the total impedance (Z) of the circuit. The impedance in an AC circuit with an inductor is given by:
Z=√R2+X2L
The current in the AC circuit can be calculated as:
I2=VZ
Since Z (impedance) is always greater than R (resistance) in an AC circuit with an inductor, we can conclude:
I2=VZ<VR=I1
Thus, I2<I1 is indeed correct.
The reason states that in an AC circuit, the inductor coil offers more resistance. This is true because the inductive reactance XL contributes to the total impedance Z, making it larger than just the resistance R. Therefore, the current I2 is reduced due to the increased total impedance.
Both the assertion and the reason are correct, and the reason correctly explains the assertion.
Both assertion and reason are correct, and the reason is the correct explanation for the assertion.
Similar Questions
When a coil is connected to a 100 V D.C. supply, the current is 2 A. When the same coil is connected to A.C. source E=100√2sinωt, the current is 1 A. Find the inductive reactance used in the circuit.
View SolutionWhen an inductor coil is connected to an ideal battery of emf 10V, a constant current 2.5 A flows. When the same inductor coil is connected to an ac source of 10V and 50 HZ then the current is 2A. Find out the inductance of the coil.
View Solution
Knowledge Check
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. The rms value of the current in the circuit is
A12.8AB13.6AC15.9AD19.5A
An AC source is connected to a capacitor. The current in the current is I. Now a dielectric slab is inserted into the capacitor , then the new current is
View SolutionAn inductor coil is connected to a 12V battery and drawing a current 24 A. This coil is connected to capacitor and an AC source of rms voltage rating 24 V in the series connection. The rms current through the circuit would found to be
View SolutionA steady 4A flows in an inductor coil when connected to a 12V source as shown in figure. If the same coil is connected to an ac source of 12V, 50rad/s a currentd of 2.4A flows in the circuit as shown in figure2. Now after these observations , a capacitor fo capacitance 150F is connected in series with the coil and with same AC source as shown in figure 3.
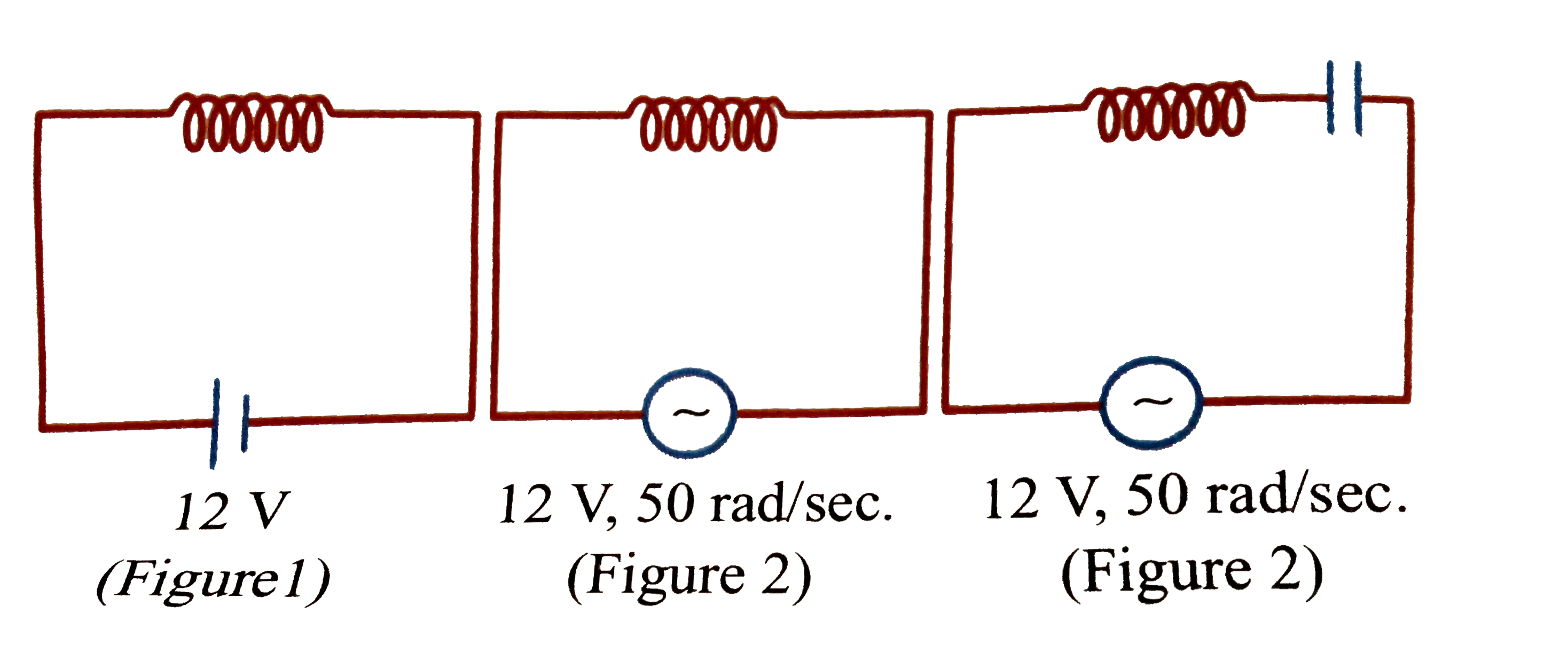
The resistance of the coil is:
View SolutionAn inductor coil joined to a 6V battery draws a steady current of 12A. This coil is connected to a capacitor and an AC source of rms voltage 6V in series. If the current in the circuit is in phase with the emf, find the rms current.
View SolutionAn inductor (L=2000mH) is connected to an AC source of peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View SolutionA 0.7 henry inductor is connected across a 120V−60HzAC source. The current in the inductor will be very nearly
View SolutionA current of 6 A flows in a coil when connected to a dc source of 18 V. If the same coil is connected to an ac source of 20 V, 50 rad/s, a current of 4 A flows in the circuit. The inductance of the coil is 10x mH. Find out the value of x.
View Solution
