If the alternating current I=I1cosωt+I2sinωt, then the rms current is given by
I1+I2√2
|I1+I2|√2
√I21+I222
⎷I21+I22√2
The correct Answer is:C
To find the RMS (Root Mean Square) current for the given alternating current I=I1cos(ωt)+I2sin(ωt), we can follow these steps:
1. Identify the Components:
The alternating current is given as:
I=I1cos(ωt)+I2sin(ωt)
Here, I1 and I2 are the amplitudes of the cosine and sine components, respectively.
2. Express the Current in Terms of a Single Amplitude:
We can express I in terms of a single amplitude I using the Pythagorean identity:
I2=I21+I22
This follows from the fact that sin2(θ)+cos2(θ)=1.
3. Calculate the RMS Value:
The RMS value of a sinusoidal current is given by:
Irms=I√2
Substituting I from the previous step, we have:
Irms=√I21+I22√2
4. Final Expression for RMS Current:
Therefore, the expression for the RMS current can be simplified to:
Irms=√I21+I22√2=√I21+I222
5. Conclusion:
The correct option for the RMS current is:
Irms=√I21+I222
The alternating current is given as:
I=I1cos(ωt)+I2sin(ωt)
Here, I1 and I2 are the amplitudes of the cosine and sine components, respectively.
We can express I in terms of a single amplitude I using the Pythagorean identity:
I2=I21+I22
This follows from the fact that sin2(θ)+cos2(θ)=1.
The RMS value of a sinusoidal current is given by:
Irms=I√2
Substituting I from the previous step, we have:
Irms=√I21+I22√2
Therefore, the expression for the RMS current can be simplified to:
Irms=√I21+I22√2=√I21+I222
The correct option for the RMS current is:
Irms=√I21+I222
Similar Questions
An alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View SolutionAn alternative current is given by I=(100√2sint)A. The RMS value of current is
View SolutionThe rms value of an alternating current
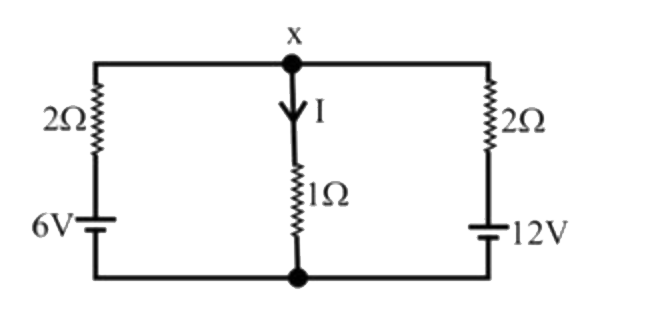
View SolutionFind the current I in the given circuit
View SolutionThe average value of alternating current I=I0sinωt in time interval [0,πω] is
View SolutionA wire carries an alternating current i=i0sinωt. In there an electric field in the vicinity of the wire?
View SolutionThe electric current in a circuit is given by I = 3 sin ωt+4cosωt. The rms current is
View SolutionIn the circuit shown, the currents i1 and i2 are
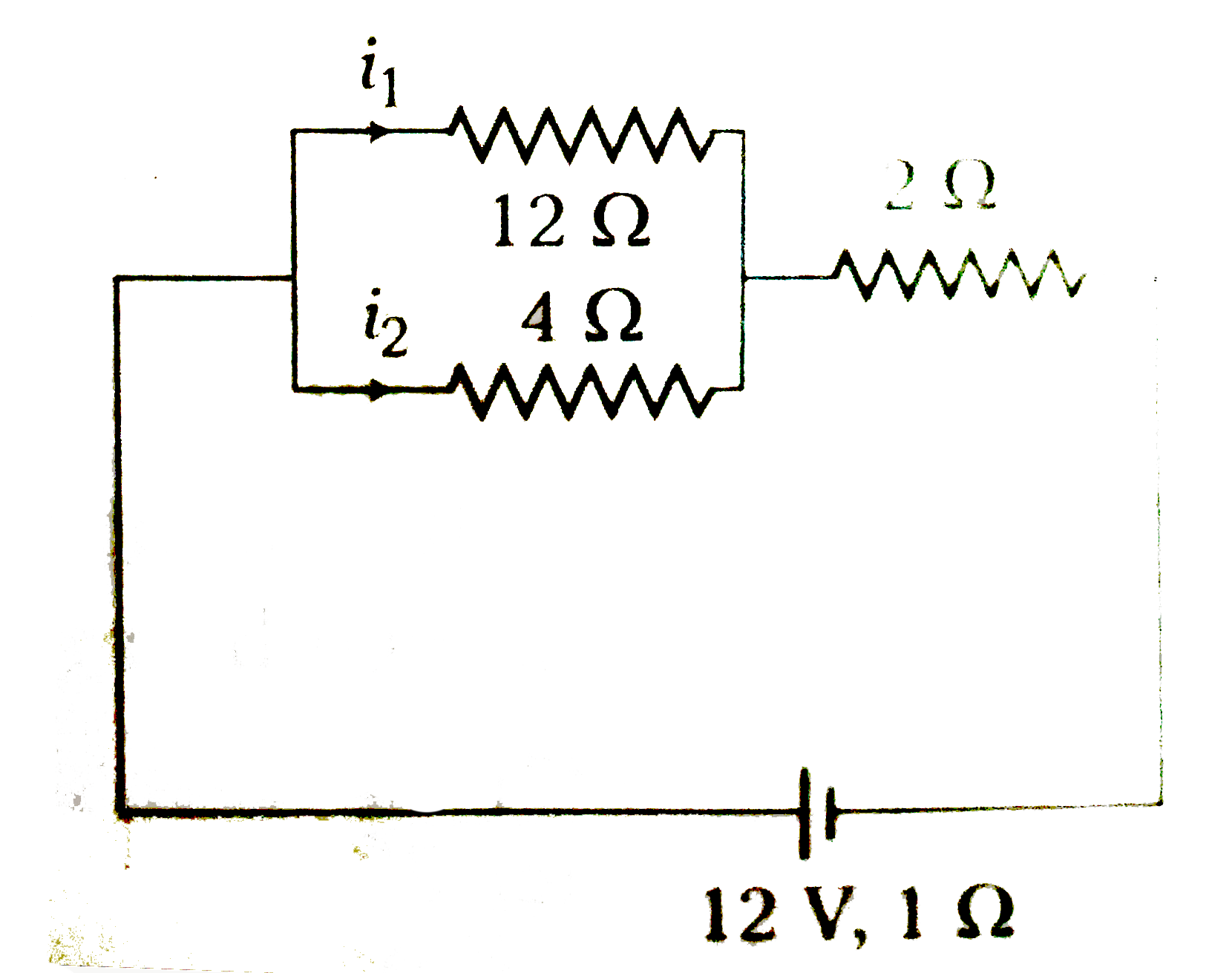
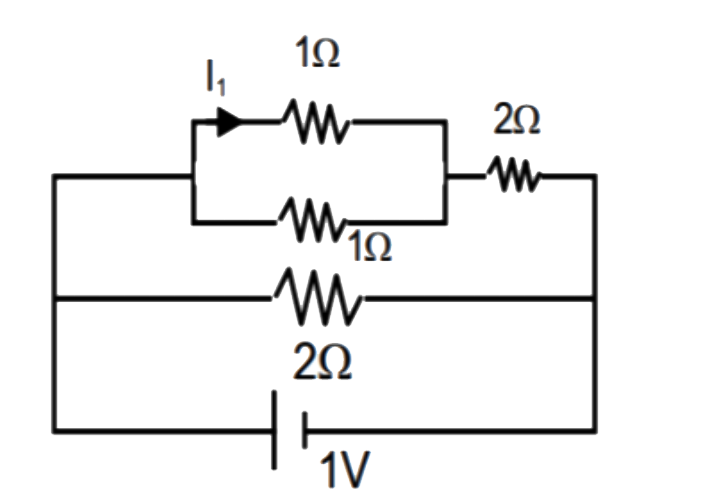
View SolutionThe current I1 (in A) flowing through the 1Ω resistor in the given circuit is
View Solution
