A light beam passes from medium 1 to medium 2. Show that the emerging beam is parallel to the incident beam.
To show that the emerging beam is parallel to the incident beam when a light beam passes from medium 1 to medium 2, we can follow these steps:
1. Understanding the Setup:
- Consider two media: Medium 1 (with refractive index μ1) and Medium 2 (with refractive index μ2).
- Let an incident ray strike the boundary between these two media at an angle I1.
2. Applying Snell's Law:
- According to Snell's Law, when light passes from one medium to another, the relationship between the angles and the refractive indices is given by:
μ1sinI1=μ2sinR
- Here, R is the angle of refraction in medium 2.
3. Refraction from Medium 2 to Medium 1:
- Now, consider the light ray traveling from medium 2 back into medium 1. Let the angle of incidence at this boundary be R (the angle we just calculated) and the angle of emergence be E.
- Again, applying Snell's Law at this boundary gives:
μ2sinR=μ1sinE
4. Setting Up the Equations:
- From the first application of Snell's Law:
sinR=μ1μ2sinI1(Equation 1)
- From the second application of Snell's Law:
sinE=μ2μ1sinR(Equation 2)
5. Substituting Equation 1 into Equation 2:
- Substitute sinR from Equation 1 into Equation 2:
sinE=μ2μ1(μ1μ2sinI1)
- This simplifies to:
sinE=sinI1
6. Concluding the Proof:
- Since sinE=sinI1, it follows that:
E=I1
- Therefore, the angle of emergence E is equal to the angle of incidence I1, which means the emerging beam is parallel to the incident beam.
Final Result:
The emerging beam is parallel to the incident beam because the angle of incidence is equal to the angle of emergence.
---
- Consider two media: Medium 1 (with refractive index μ1) and Medium 2 (with refractive index μ2).
- Let an incident ray strike the boundary between these two media at an angle I1.
- According to Snell's Law, when light passes from one medium to another, the relationship between the angles and the refractive indices is given by:
μ1sinI1=μ2sinR
- Here, R is the angle of refraction in medium 2.
- Now, consider the light ray traveling from medium 2 back into medium 1. Let the angle of incidence at this boundary be R (the angle we just calculated) and the angle of emergence be E.
- Again, applying Snell's Law at this boundary gives:
μ2sinR=μ1sinE
- From the first application of Snell's Law:
sinR=μ1μ2sinI1(Equation 1)
- From the second application of Snell's Law:
sinE=μ2μ1sinR(Equation 2)
- Substitute sinR from Equation 1 into Equation 2:
sinE=μ2μ1(μ1μ2sinI1)
- This simplifies to:
sinE=sinI1
- Since sinE=sinI1, it follows that:
E=I1
- Therefore, the angle of emergence E is equal to the angle of incidence I1, which means the emerging beam is parallel to the incident beam.
The emerging beam is parallel to the incident beam because the angle of incidence is equal to the angle of emergence.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.1
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 10 cm apart with their principal axes coinciding. A beam of light travelling parallel to the principal axis and having a beam diameter 5.0 mm, is incident on the combination. Show that the emergent beam is parallel to the incident one. Find the beam diameter of the emergent beam.
View SolutionA beam of light passes from medium 1 to medium 2 to medium 3 as shown figure. What may be concluded about the three indices of refraction, n1,n2,andn3 ?
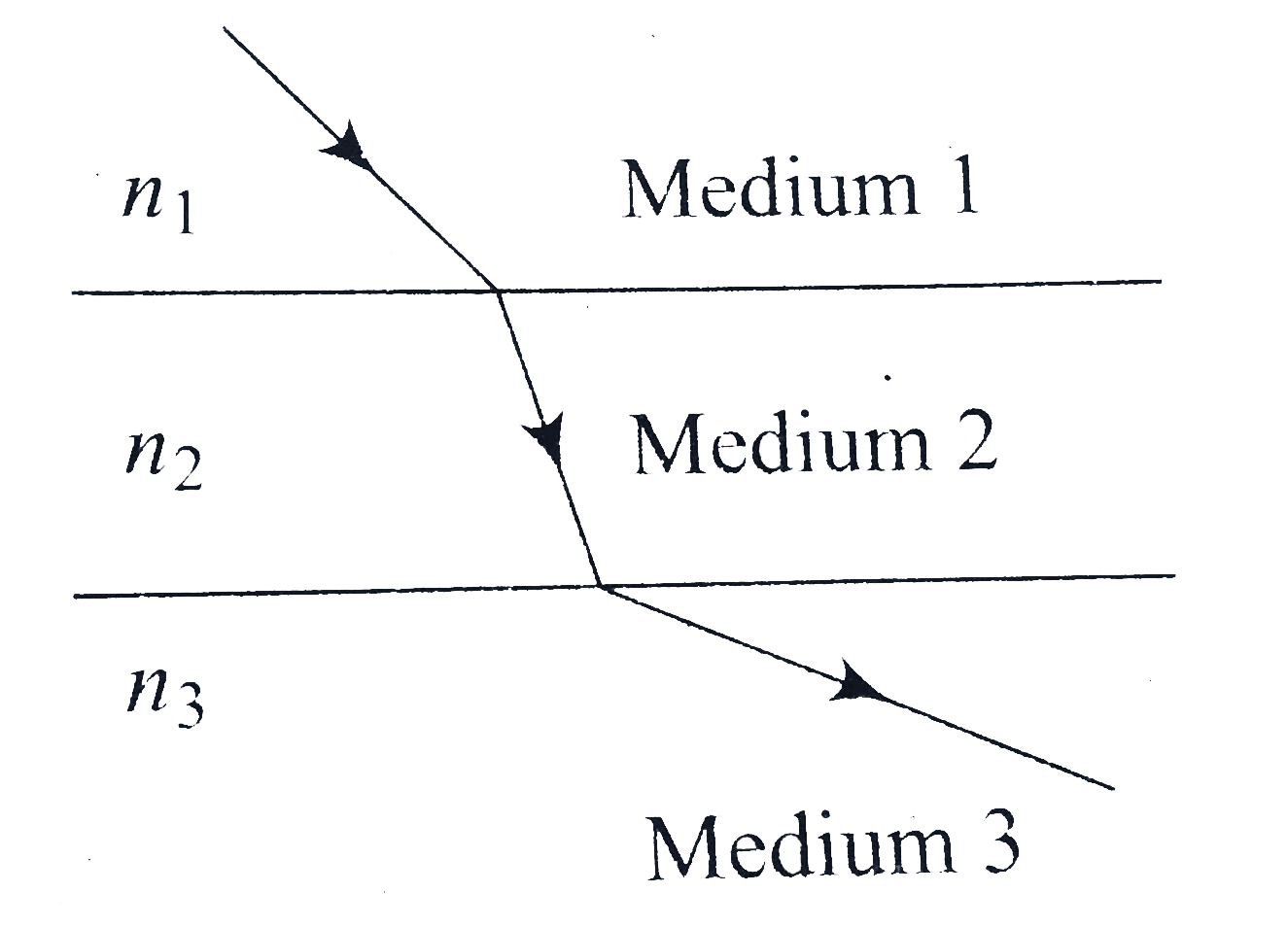
View Solution
Knowledge Check
A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incidence is :
A0∘B45∘C60∘D90∘
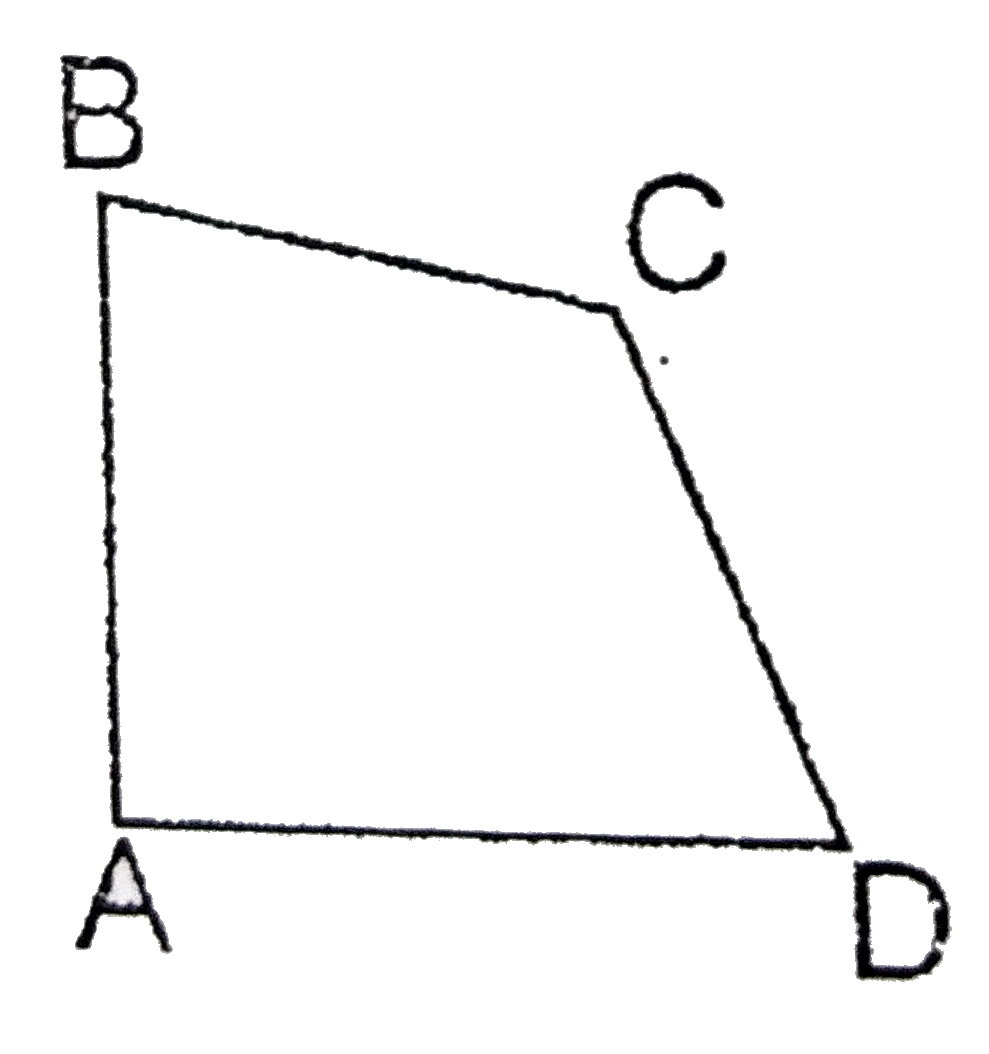
In the given figure, the faces of prism ABCD made of glass with a refractive index n form dihedral angles ∠A=90∘,∠B75∘,,∠C=135∘&∠D=60∘ (The Abbe's prism) .A beam of light falls on face AB & after total internal reflection from face BC escapes through face AD.Find the range of n and angle of incidence α of the beam onto face AB, if a beam that has passed through the prism in this mahner is perpedicular to the incident beam.
View SolutionWhen a beam of light is incident on a plane mirror, it is found that a real image is formed. The incident beam must be
View SolutionWhen a beam of light goes from denser medium (μd) to rarer medium (μr), then it is generally observed that magnitude of angle of incidence is half that of angle of refraction. Then magnitude of incident angle will be-(here μ=μd/μr)
View SolutionRefractive index of the material of concave lens is μ. The lens is immersed inb a medium of refractive index μ1(μ1>μ). A parallel beam of light is incident on the lens. Draw a diagram to show the path of emergent rays.
View SolutionA beam of light propagates through a medium 1 and falls onto another medium 2, at an angle α1 as shown in figure. After that, it propagates in medium 2 at an angle α2 as shown. The light's wavelength in medium 1 is λ1. What is the wavelength of light in medium
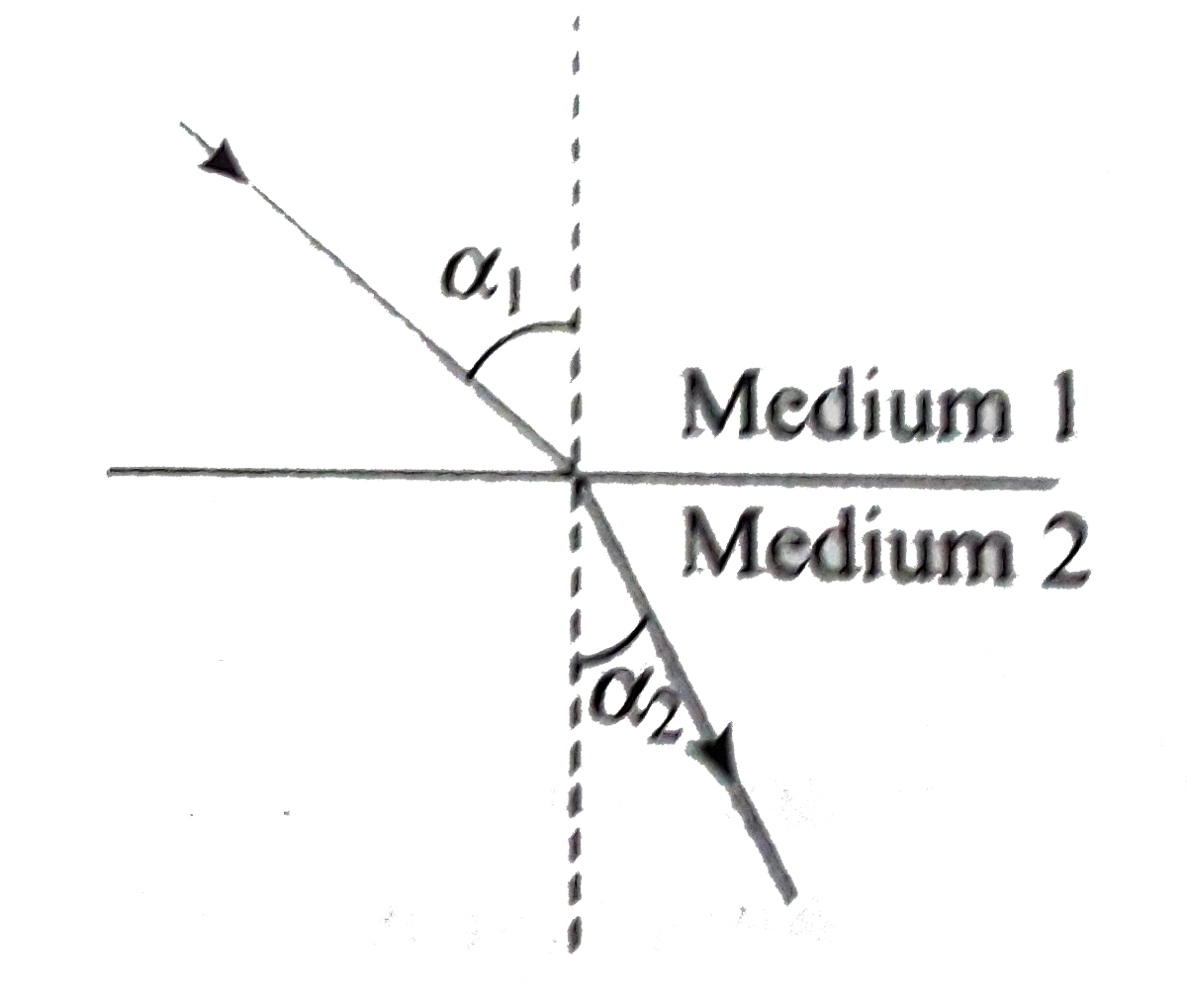
View SolutionA parallel beam of light falls normally on the first face of a prism of small angle .At the second face it is partly reflected,the reflected beam striking at the first face again, and emerging from it in a direction making an angle 6∘ 30' with the reversed direction of the incident beam. The refracted beam is found to have undergone a deviation of 1∘15' from the original direction.Find the refractive index of the glass and the angle of the prism.
View SolutionA parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Show that if the incident beam makes an angle θ=sin−1(λ2d) with the normal to the plane of the slits, there will be a dark fringe at the centre Po of the pattern.
View Solution
