Absolute refractive indices of glass and water are 3/2 and 4/3. The ratio of velocity of light in glass and water will be
4:3
9:8
8:9
3:4
The correct Answer is:C
To find the ratio of the velocity of light in glass and water given their absolute refractive indices, we can follow these steps:
Step 1: Understand the relationship between refractive index and velocity of light
The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (C) to the speed of light in that medium (V). This can be expressed as:
μ=CV
From this, we can rearrange the formula to find the velocity of light in the medium:
V=Cμ
Step 2: Write the expression for the ratio of velocities
We need to find the ratio of the velocity of light in glass (V_g) to the velocity of light in water (V_w):
VgVw=C/μgC/μw
Here, μ_g is the refractive index of glass, and μ_w is the refractive index of water.
Step 3: Simplify the expression
Since C (the speed of light in vacuum) is a common factor in both the numerator and the denominator, it cancels out:
VgVw=μwμg
Step 4: Substitute the given refractive indices
From the problem, we know:
- Refractive index of glass (μ_g) = 32
- Refractive index of water (μ_w) = 43
Substituting these values into the ratio:
VgVw=4332
Step 5: Simplify the fraction
To simplify the fraction, we multiply by the reciprocal of the denominator:
VgVw=43×23=89
Conclusion
Thus, the ratio of the velocity of light in glass to the velocity of light in water is:
VgVw=89
Final Answer
The ratio of the velocity of light in glass and water is 89.
---
The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (C) to the speed of light in that medium (V). This can be expressed as:
μ=CV
From this, we can rearrange the formula to find the velocity of light in the medium:
V=Cμ
We need to find the ratio of the velocity of light in glass (V_g) to the velocity of light in water (V_w):
VgVw=C/μgC/μw
Here, μ_g is the refractive index of glass, and μ_w is the refractive index of water.
Since C (the speed of light in vacuum) is a common factor in both the numerator and the denominator, it cancels out:
VgVw=μwμg
From the problem, we know:
- Refractive index of glass (μ_g) = 32
- Refractive index of water (μ_w) = 43
VgVw=4332
To simplify the fraction, we multiply by the reciprocal of the denominator:
VgVw=43×23=89
Thus, the ratio of the velocity of light in glass to the velocity of light in water is:
VgVw=89
The ratio of the velocity of light in glass and water is 89.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.420videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.510videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.210videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
The absolute refractive indices of glass and water are 32and43 respectively. If the
speed of light is 2×108m/s, calucalate the speed of light in (i) vacuum, (ii) water.View SolutionA light wave travels from glass to water. The refractive index for glass and water are 32 and 43 respectively. The value of the critical angle will be:
View SolutionIf refractive index of glass is 1.50 and of water is 1.33, then criticle angle is
View SolutionThe refractive index of glass with respect to water is 98. If the velocity of wavelength of light in glass are 2×108m/s and 4000 Å respectively, find the velocity and wavelength of light in water.
View SolutionA beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
View SolutionThe refractive index of glass is 3/2. What is the polarising angle for glass
View SolutionThe refractive index of water is 4/3. The speed of light in water is
View SolutionLight is incident from air on an oil layer at an incident angle of 30∘. After moving through the oil 1, oil 2, and glass it enters water. If the refraction index of glass and water are 1.5 and 1.3, respectively. Find the angle which the ray makes with the normal in water.
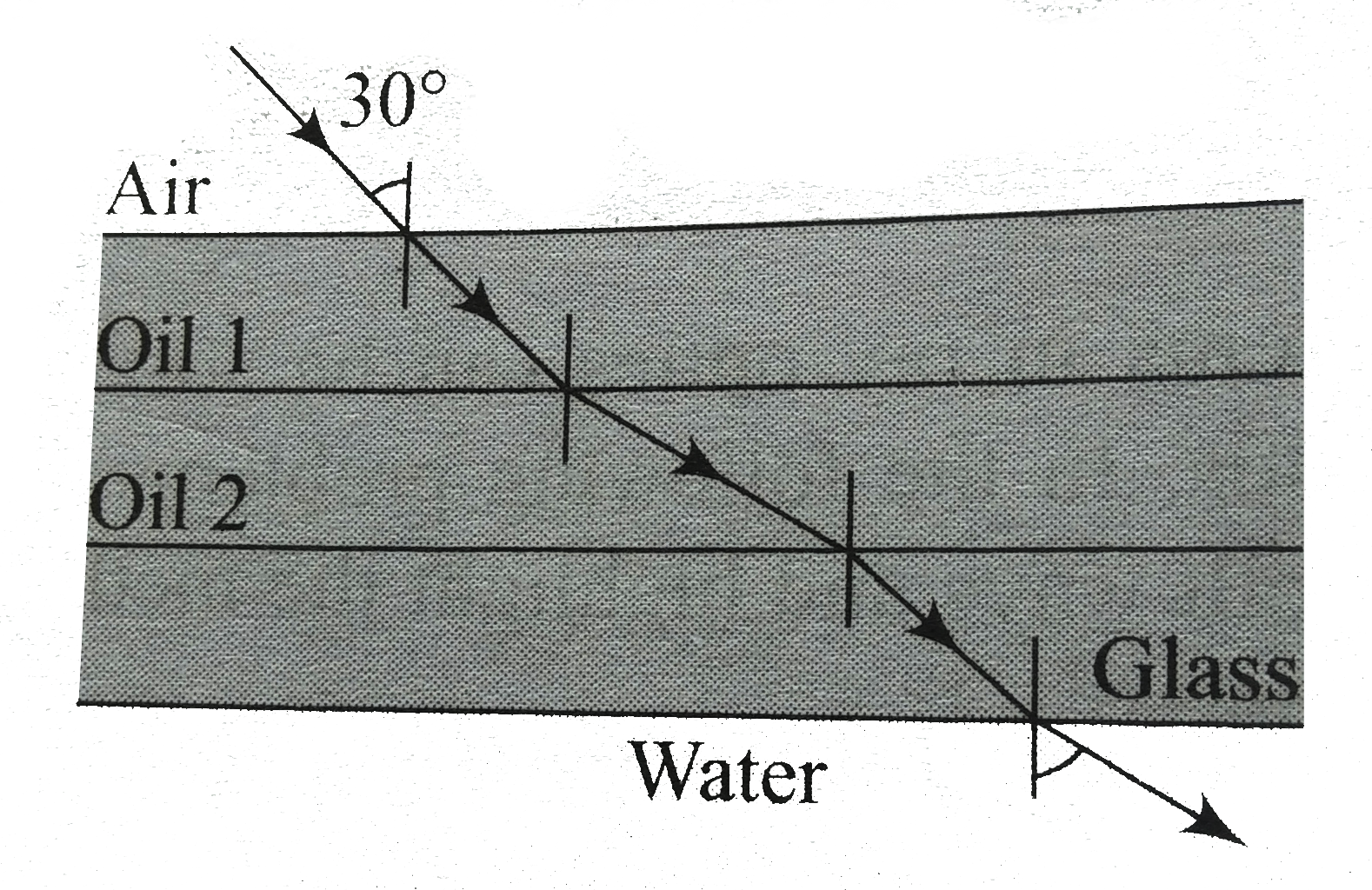 View Solution
View SolutionFill in the blanks to complete the following sentence:
Q: The refractive index of glass with respect to air is 3/2. thee refractive index of air with respect to glass will be _____View SolutionElectromagnetic radiation of frequency v, velocity v and wavelength λ in air, enters a glass slab of refractive index μ . The frequency, wavelength and velocity of light in the glass slab will be, respectively
View Solution

