An air bubble inside a glass slab (µ=1.5) appears 6 cm when viewed from one side and 4 cm when viewed from the opposite side. The thickness of the slab is
10 cm
6.67 cm
15 cm
None of these
The correct Answer is:C
To find the thickness of the glass slab containing an air bubble, we can use the apparent depth formula and the concept of refraction. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have an air bubble inside a glass slab with a refractive index (µ) of 1.5. The bubble appears to be 6 cm deep when viewed from one side and 4 cm deep when viewed from the opposite side.
Step 2: Define Variables
Let:
- d1 = apparent depth when viewed from one side = 6 cm
- d2 = apparent depth when viewed from the opposite side = 4 cm
- t = thickness of the glass slab (what we need to find)
- dactual = actual depth of the bubble
Step 3: Use the Formula for Apparent Depth
The relationship between the actual depth and the apparent depth can be expressed as:
dapparent=dactualμ
Where μ is the refractive index of the medium (glass in this case).
Step 4: Calculate Actual Depth from Each Side
1. From the first side:
dactual1=d1×μ=6cm×1.5=9cm
2. From the second side:
dactual2=d2×μ=4cm×1.5=6cm
Step 5: Relate Actual Depths to Thickness
The total thickness of the slab can be found by adding the actual depths from both sides:
t=dactual1+dactual2
Substituting the values we calculated:
t=9cm+6cm=15cm
Final Answer
The thickness of the glass slab is 15 cm.
---
We have an air bubble inside a glass slab with a refractive index (µ) of 1.5. The bubble appears to be 6 cm deep when viewed from one side and 4 cm deep when viewed from the opposite side.
Let:
- d1 = apparent depth when viewed from one side = 6 cm
- d2 = apparent depth when viewed from the opposite side = 4 cm
- t = thickness of the glass slab (what we need to find)
- dactual = actual depth of the bubble
The relationship between the actual depth and the apparent depth can be expressed as:
dapparent=dactualμ
Where μ is the refractive index of the medium (glass in this case).
1. From the first side:
dactual1=d1×μ=6cm×1.5=9cm
2. From the second side:
dactual2=d2×μ=4cm×1.5=6cm
The total thickness of the slab can be found by adding the actual depths from both sides:
t=dactual1+dactual2
Substituting the values we calculated:
t=9cm+6cm=15cm
The thickness of the glass slab is 15 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.4
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.5
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
An air bubble in a glass slab with refractive index 1.5 (near normal incidence) is 5cm deep when viewed from one surface and 3cm deep when viewed from the opposite face. The thickness (in cm) of the slab is
View SolutionA bubble in glass slab (μ=1.5) when viewed from one side appears at 5 cm and 2 cm from other side, then thickness of slab is :
View Solution
Knowledge Check
A small air bubble in a glass block when seen from above appears to be raised because of :
Arefraction of lightBreflection of lightCreflection and refraction of lightDnone of the above
An air bubble trapped inside a rectangular glass slab (cuboid) appear at 2 cm from one side and at 3 cm from the other opposite side. If the refractive index of glass is 1.5, what is the actual width of the glass slab?
View SolutionThe image of point P when viewed from top of the slabs will be
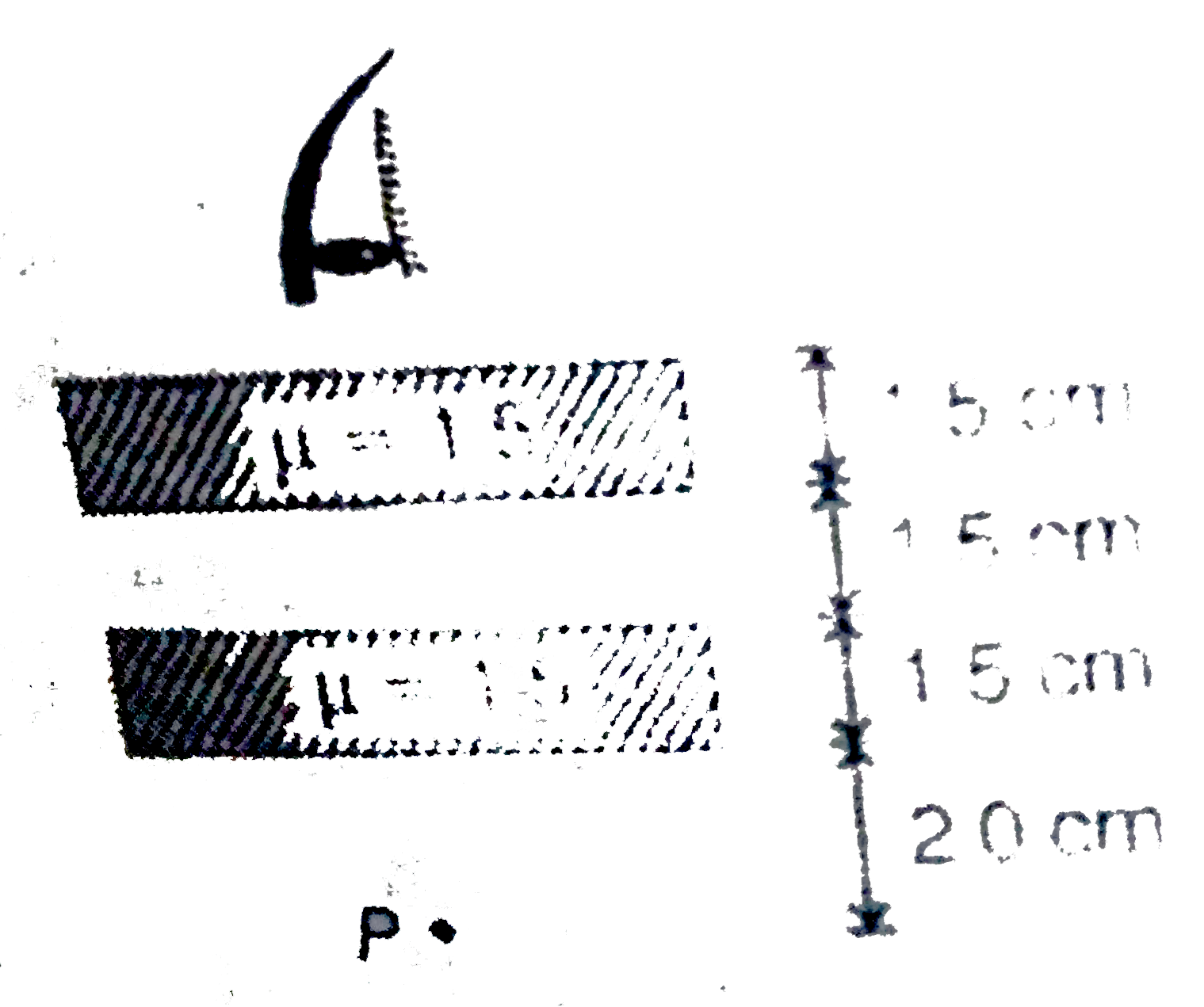
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA transparent cube of 15cm edge contains a small air bubble. Its apparent depth when viewed through one face is 6cm and when viewed through the opposite face is 4cm. Then the refractive index of the material of the cube is
View SolutionA transparent cube of 15cm edge contains a small air bubble. Its apparent depth when viewed through one face is 6cm and when viewed through the opposite face is 4cm. Then the refractive index of the material of the cube is
View SolutionA transparent cube of side 210mm contains a small air bubble. Its apparent distance, when viewed from one face of the cube is 100mm, and when viewed through opposite face is 40mm. What is the actual distance of the bubble from the second face and what is the refractive index of the material of the cube ?
View SolutionThere is small air bubble inside a glass sphere (μ=1.5) of radius 5cm. The bubble is at 'O' at 7.5cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10cm below the surface of water. The bubble is viewed normally from air. Find the apperent depth of the bubble.

View Solution
