If the critical angle for total internal reflection, from a medium to vacuum is 30∘, then velocity of light in the medium is
1.5×108m/s
2×108m/s
3×108m/s
6×108m/s
The correct Answer is:1
To find the velocity of light in the medium given the critical angle for total internal reflection, we can follow these steps:
1. Understand the Concept of Critical Angle:
The critical angle (C) is the angle of incidence in a denser medium (with refractive index μ) at which the angle of refraction in a rarer medium (with refractive index 1, for vacuum) is 90 degrees.
2. Use the Relationship Between Refractive Index and Critical Angle:
The relationship between the refractive index (μ) and the critical angle (C) is given by:
μ=1sinC
3. Substitute the Given Critical Angle:
We are given that the critical angle C=30∘. Therefore, we can calculate sin30∘:
sin30∘=12
Now substituting this value into the formula for refractive index:
μ=1sin30∘=112=2
4. Relate Refractive Index to Velocity of Light:
The refractive index is also related to the speed of light in vacuum (c) and the speed of light in the medium (v) by the formula:
μ=cv
Rearranging this gives us:
v=cμ
5. Substitute the Values:
We know that the speed of light in vacuum c=3×108 m/s and μ=2:
v=3×1082=1.5×108 m/s
6. Conclusion:
The velocity of light in the medium is 1.5×108 m/s.
Final Answer:
The velocity of light in the medium is 1.5×108 m/s.
---
The critical angle (C) is the angle of incidence in a denser medium (with refractive index μ) at which the angle of refraction in a rarer medium (with refractive index 1, for vacuum) is 90 degrees.
The relationship between the refractive index (μ) and the critical angle (C) is given by:
μ=1sinC
We are given that the critical angle C=30∘. Therefore, we can calculate sin30∘:
sin30∘=12
Now substituting this value into the formula for refractive index:
μ=1sin30∘=112=2
The refractive index is also related to the speed of light in vacuum (c) and the speed of light in the medium (v) by the formula:
μ=cv
Rearranging this gives us:
v=cμ
We know that the speed of light in vacuum c=3×108 m/s and μ=2:
v=3×1082=1.5×108 m/s
The velocity of light in the medium is 1.5×108 m/s.
The velocity of light in the medium is 1.5×108 m/s.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-D
9 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
If critical angle for TIR from medium to vacuum is 45 deg then velocity of light in medium
View SolutionDefine critical angle for a given medium
View SolutionHow is the critical angle related to the refractive index of a medium ?
View SolutionDraw a labelled ray diagram to illustrate (a) critical angle (b) total internal reflection for a ray of light moving from one medium to another.
View SolutionA ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
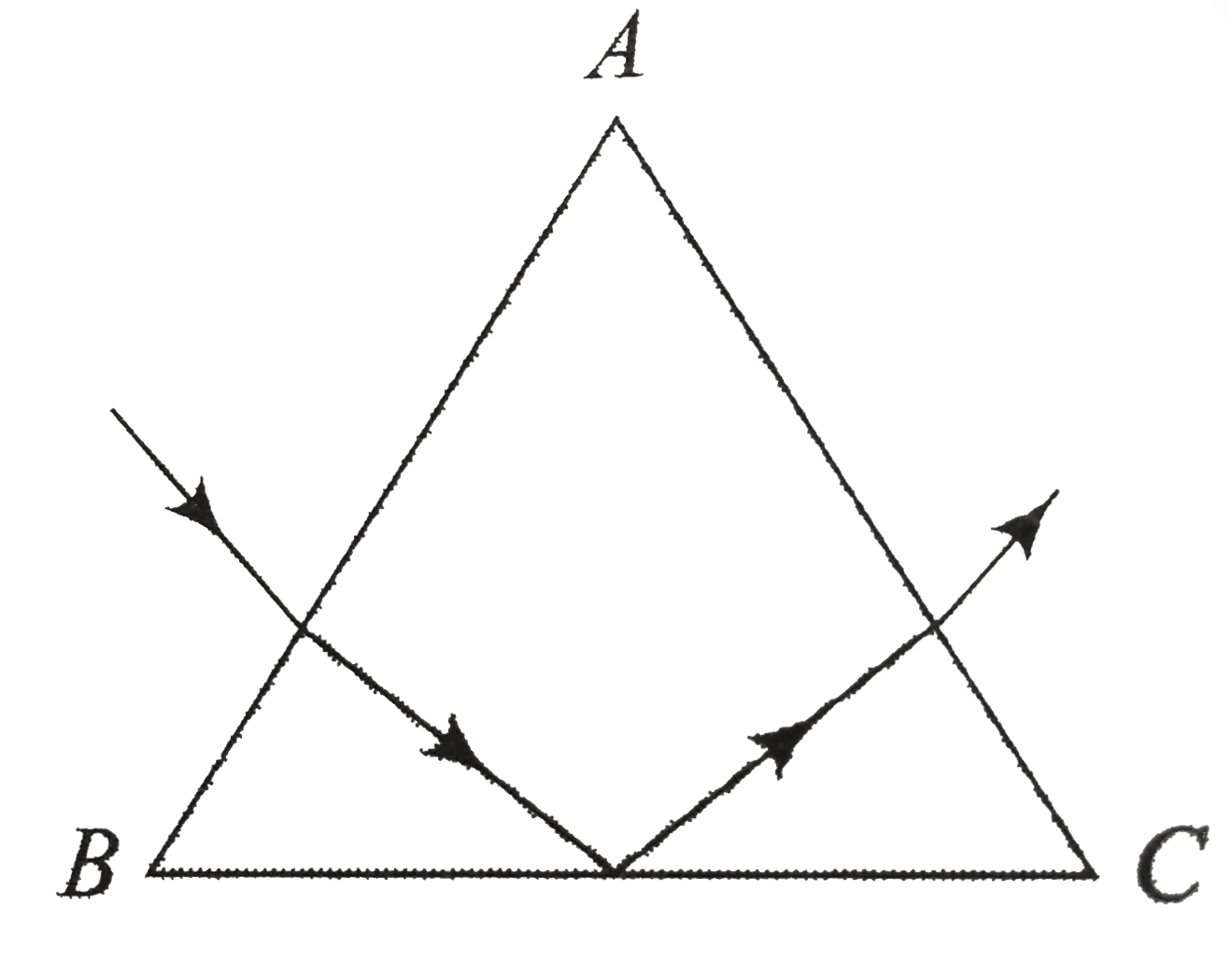
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
View SolutionHow is the refractive index of a material related to:
Velocity of light in vacuum or air and the velocity of light in a given medium?
View SolutionThe critical angle for light going from medium X into medium Y is θ . The speed of light in medium X is v. The speed of light in medium Y is
View SolutionWave length of light in denser mediumis 4000Å, it is grazing into a rarer medium. If critical angle for the pairof mediam is sin−1(23) then the wave length of light in rarer medium is
View SolutionWhen light is incident on a medium at angle i and refracted into a second medium at an angle r, the graph of sinr versus sini is as shown. From this one can conclude that

(i) the velocity of light in second medium is √3 times the velocity of light in the first medium
(ii) the velocity of light in the first medium is √3 times the velocity of ligth in second medium
(iii) the critical angle of the two media is given by siniC=1√3
(iv) the critical anlge of the two media is given by siniC=1√2
View Solution
