A beam of electrons of energy E scatters from a target having atomic specing of 1Å. The first maximum intensity occurs at θ=60∘. The E (in eV) is ___________
(Planck constant h=6.64×10−34Js,
1eV=1.6×1019J,
electron mass m=9.1×10−31kg)
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between the de Broglie wavelength and the energy of the electrons.
The de Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle. For an electron, the momentum can be expressed in terms of its mass (m) and velocity (v):
p=mv
Step 2: Relate the energy of the electron to its momentum.
The kinetic energy (E) of the electron is given by:
E=12mv2
From this, we can express the momentum in terms of energy:
E=p22m⟹p=√2mE
Step 3: Substitute the expression for momentum into the de Broglie wavelength formula.
Substituting p into the de Broglie wavelength formula gives:
λ=h√2mE
Step 4: Use Bragg's law to relate the wavelength to the atomic spacing.
According to Bragg's law, the condition for constructive interference (first maximum) is given by:
2dsinθ=λ
where d is the atomic spacing and θ is the scattering angle. Given d=1Å=1×10−10m and θ=60∘, we can calculate sin60∘=√32:
λ=2dsinθ=2×(1×10−10)×√32=√3×10−10m
Step 5: Equate the two expressions for the de Broglie wavelength.
Now we have:
√3×10−10=h√2mE
Squaring both sides:
3×10−20=h22mE
Step 6: Solve for the energy E.
Rearranging the equation gives:
E=h22m×3×10−20
Step 7: Substitute the values of h and m.
Using h=6.64×10−34Js and m=9.1×10−31kg:
E=(6.64×10−34)22×(9.1×10−31)×(3×10−20)
Step 8: Calculate E in Joules and convert to electron volts.
Calculating the above expression:
E=4.4096×10−675.46×10−50≈8.06×10−18J
Now converting Joules to electron volts:
E (in eV)=8.06×10−181.6×10−19≈50.375eV
Final Answer:
The energy E in electron volts is approximately:
E≈50.47eV
---
λ=hp
where h is Planck's constant and p is the momentum of the particle. For an electron, the momentum can be expressed in terms of its mass (m) and velocity (v):
p=mv
E=12mv2
From this, we can express the momentum in terms of energy:
E=p22m⟹p=√2mE
λ=h√2mE
2dsinθ=λ
where d is the atomic spacing and θ is the scattering angle. Given d=1Å=1×10−10m and θ=60∘, we can calculate sin60∘=√32:
λ=2dsinθ=2×(1×10−10)×√32=√3×10−10m
√3×10−10=h√2mE
Squaring both sides:
3×10−20=h22mE
E=h22m×3×10−20
E=(6.64×10−34)22×(9.1×10−31)×(3×10−20)
E=4.4096×10−675.46×10−50≈8.06×10−18J
Now converting Joules to electron volts:
E (in eV)=8.06×10−181.6×10−19≈50.375eV
The energy E in electron volts is approximately:
E≈50.47eV
Topper's Solved these Questions
Similar Questions
A neutron beam of energy E scatters from atoms on a surface with a spacing d=0.1nm. The first maximum of intensity in the reflected beam occurs at θ=30∘. What is the kinetic energy of E of the beam in eV?
View SolutionIf the kinetic energy of an electron is 4.55×10−25J, find its wavelength (Planck's cosntant, h=6.625×10−34kgm2s−1,m=9.1×10−31kg).
View Solution
Knowledge Check
Uncertainty in position of a particle of 25 g in space is 10−5 m. Hence, uncertainty in velocity (ms−1) is (Planck's constant h=6.6×10−34Js)
A2.1×10−28B2.1×10−34C0.5×10−34D5.0×10−24in the question number 63, the frequency of emitted photon due to the given transition is (h=6.64×10−34Js,1eV=1.6×10−19J)
A2.46×1010HzB2.46×1012HzC2.46×1015HzD2.46×1018Hz
When an electron in hydrogen atom is excited, from its 4th to 5th stationary orbit, the change in angular momentum of electron is (Planck's constant: h=6.6×10−34J−s)
View SolutionAn electron beam has a kinetic energy equal to 100 eV . Find its wavelength associated with a beam , if mass of electron =9.1×10−31 kg and 1 eV =1.6×10−19J . (Planks's constant = 6.6×10−34J−s)
View SolutionIf de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given h=6.6×10−34 Js ,
e=1.6×10−19 C, me=9.11×10−31 kg.
View SolutionIn an experiment tungsten cathode which has a threshold 2300Å is irradiated by ultraviolet light of wavelength 1800Å. Calculate
(i) Maximum energy of emitted photoelectron and
(ii) Work function for tungsten.
(Mention both the results in electron-volts)
Given Planck's constant h=6.6×10−34J−sec, 1eV=1.6×10−19J and velocity of light c=3×108m/sec
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
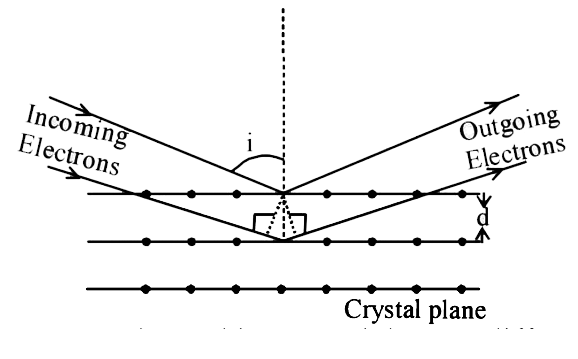
Electron accelerated by potential V are diffracted from a crystal if d=1Åandi=30∘,V should be about (h=6.6×10−34Js,me=9.1×10−31kg,e=1.6×10−19C)
View SolutionWhat is the number of significant figures in Avogadro's number (6.0×1023) and Planck's constant (6.62×10−34Js).
View Solution
