The outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of the coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
The correct Answer is:4
To solve the problem, we need to find the minimum value of K given the conditions of destructive interference for light reflected from the upper and lower surfaces of a thin coating of refractive index μC=1.6 on a glass slab of refractive index μS=1.5.
1. Understanding the Problem:
- We have a thin coating of refractive index μC=1.6 on a glass slab with refractive index μS=1.5.
- Orange light of wavelength λ=6400Å=6400×10−10m is incident normally on the coating.
- The thickness of the coating is given as t=5K×10−8m.
2. Condition for Destructive Interference:
- For destructive interference, the path difference between the light reflected from the upper surface and the lower surface of the coating must be an odd multiple of half the wavelength:
Δx=2tμC−λ2=(2n−1)λ2
- Here, n is an integer representing the order of interference.
3. Calculating the Path Difference:
- The path difference can be expressed as:
Δx=2μCt−λ2
- Setting this equal to the condition for destructive interference:
2μCt−λ2=(2n−1)λ2
4. Rearranging the Equation:
- Rearranging gives:
2μCt=(2n)λ2
- Simplifying this, we have:
μCt=nλ2
5. Substituting Values:
- Substituting μC=1.6 and λ=6400×10−10m:
1.6t=n6400×10−102
- For the minimum value of K, we take n=1:
1.6t=1⋅6400×10−102
- This simplifies to:
1.6t=3200×10−10
6. Solving for Thickness t:
- Solving for t:
t=3200×10−101.6=2000×10−10m=2×10−7m
7. Relating Thickness to K:
- We know t=5K×10−8:
2×10−7=5K×10−8
- Dividing both sides by 10−8:
20=5K
- Therefore, solving for K:
K=205=4
Final Answer:
The minimum value of K is 4.
- We have a thin coating of refractive index μC=1.6 on a glass slab with refractive index μS=1.5.
- Orange light of wavelength λ=6400Å=6400×10−10m is incident normally on the coating.
- The thickness of the coating is given as t=5K×10−8m.
- For destructive interference, the path difference between the light reflected from the upper surface and the lower surface of the coating must be an odd multiple of half the wavelength:
Δx=2tμC−λ2=(2n−1)λ2
- Here, n is an integer representing the order of interference.
- The path difference can be expressed as:
Δx=2μCt−λ2
- Setting this equal to the condition for destructive interference:
2μCt−λ2=(2n−1)λ2
- Rearranging gives:
2μCt=(2n)λ2
- Simplifying this, we have:
μCt=nλ2
- Substituting μC=1.6 and λ=6400×10−10m:
1.6t=n6400×10−102
- For the minimum value of K, we take n=1:
1.6t=1⋅6400×10−102
- This simplifies to:
1.6t=3200×10−10
- Solving for t:
t=3200×10−101.6=2000×10−10m=2×10−7m
- We know t=5K×10−8:
2×10−7=5K×10−8
- Dividing both sides by 10−8:
20=5K
- Therefore, solving for K:
K=205=4
The minimum value of K is 4.
Topper's Solved these Questions
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
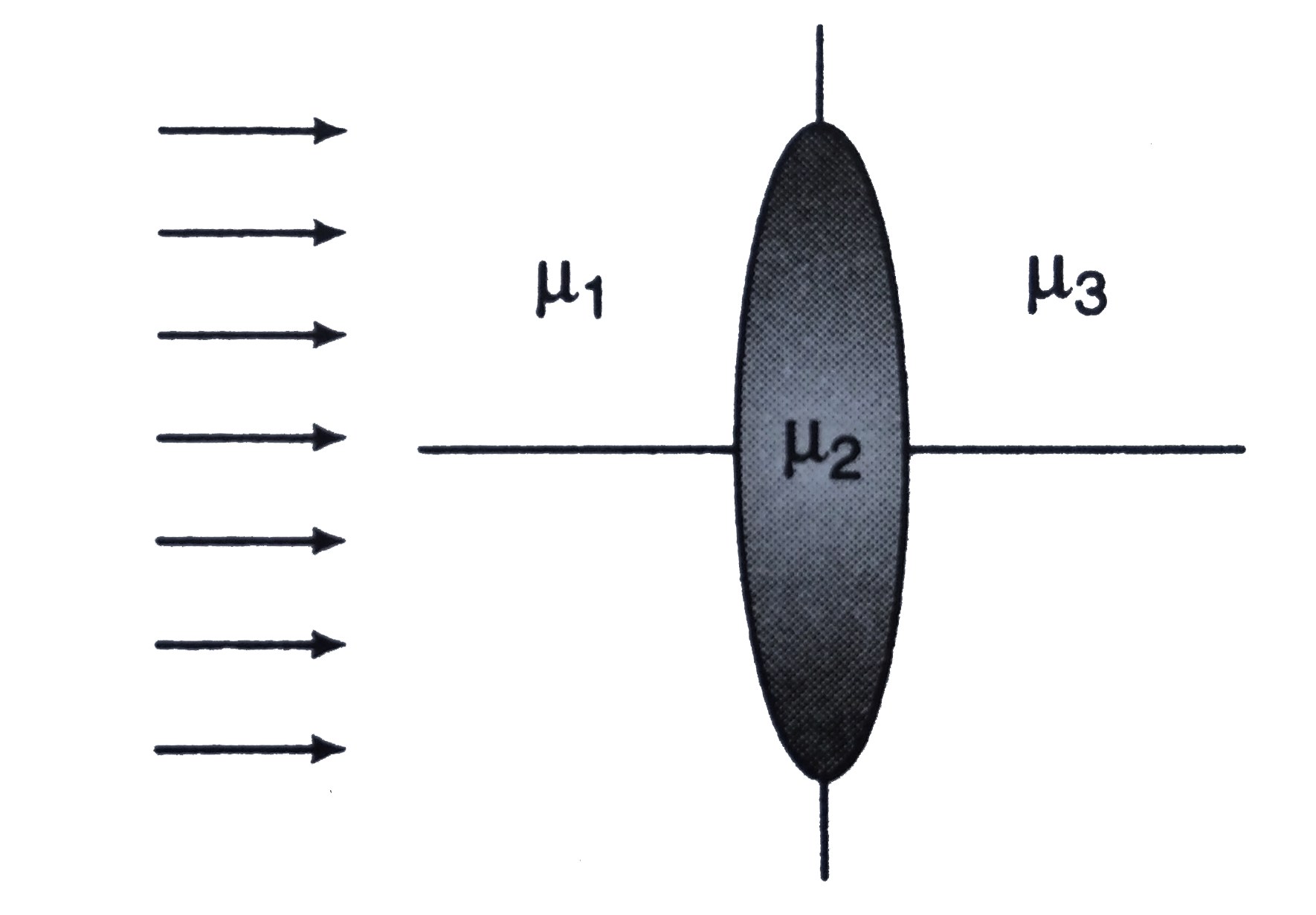
View SolutionA thin glass lens of refractive index μ2=1.5 behaves as an interface between two media of refractive indices μ1=1.4andμ3=1.6 respectively. Determine the focal length of the lens for the shown arrangement of radius of curvature of both surfaces 20cm.
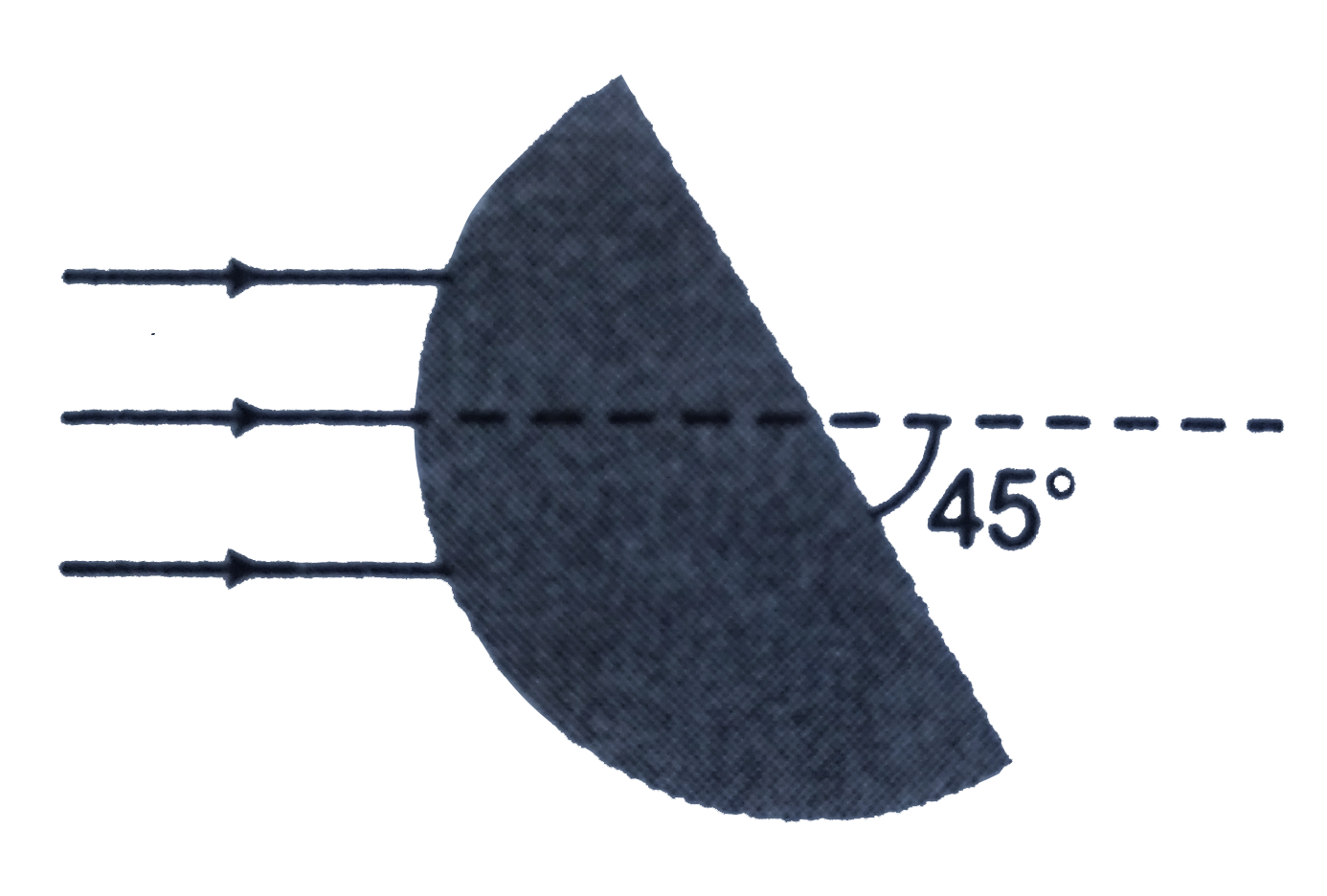
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
View SolutionA transparent glass sphere of radius 10 cm and refractive index μ=1.5 has its one half silvered so that it acts like a concave mirror. Find the position of final image for an object O at (a) 30 cm to the left of the front surface of the ball.

View SolutionA thick glass slab (μ=1.5) is to be viewed in reflected white light. It is proposed to coat the slab with a thin layer of a material having refractive index 1.3 so that the wavelength 6000 Å os suppressed. Find the minimum thickness of the coating required.
View SolutionA thin film of thickness t and index of refractive 1.33 coats a glass with index of refraction 1.50.What is the least thickness t that will strong reflect light with wavelength 600nm incident normally?
View SolutionA ray of light travelling in a transparent medium f refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ the ray can undergo total internal reflection ?
View Solution
